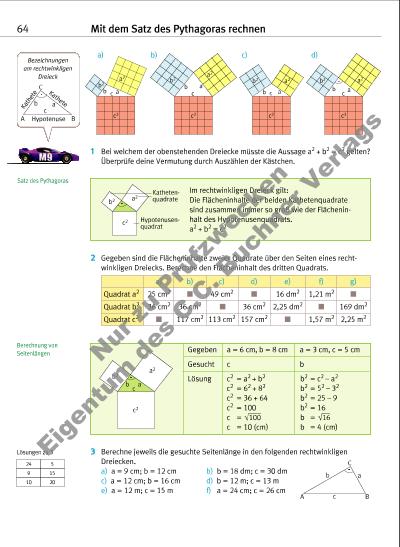
| Volltext anzeigen | |
Zeichne ein beliebiges, nicht zu kleines rechtwinkliges Dreieck und die Quadrate über den Seiten. Suche den Mittelpunkt des größeren Kathetenquadrats und zeichne durch diesen die Parallele und die Senkrechte zur Hypotenuse. Schneide nun die Teile 1–5 aus und lege damit das Hypotenusenquadrat aus. Was kannst du damit nachweisen? Begründe. Zeichne vier beliebige, gleich große rechtwinklige Dreiecke. Beschrifte jeweils die Katheten mit a und b, die Hypotenuse mit c. Stelle dann aus einem anders farbigen Papier ein Quadrat her, dessen Seitenlänge so groß ist wie die Länge der beiden Katheten zusammen (a + b). Decke das Quadrat mit den Vierecken nacheinander auf die beiden obenstehenden Arten ab. Betrachte die übrig gebliebenen Flächenteile. Wieso können sie den Satz des Pythagoras beweisen? Pythagoras von Samos war ein berühmter griechischer Mathematiker. Er lebte im 6. Jahrhundert vor Christus, also vor mehr als 2 500 Jahren. Bekannt ist sein Satz über die Seitenlängen beim rechtwinkligen Dreieck. Pythagoras hat die Richtigkeit des nach ihm benannten Satzes aber gar nicht als erster erkannt. Zu seinen Lebzeiten war diese Formel schon seit mehr als 1 000 Jahren bekannt. Schon die Chinesen, die Ägypter und die Babylonier arbeiteten mit dieser Erkenntnis. Für den Satz des Pythagoras gibt es eine Vielzahl von Beweisideen. Oben siehst du den klassischen Beweis, den du schon kennengelernt hast. Versuche ihn noch einmal zu erklären. Zwei weitere kannst du hier selbst ausprobieren. Den Satz des Pythagoras beweisen 65 5 1 2 4 3 4 3 2 1 5 a b c a b c ab 1 2 3 4 5 6 7 8 9 10 1112 1314 15 16 17 1819 20 2122 2324 25 13 14 1516 9 10 1112 5 6 7 8 1 2 3 4 7 8 9 4 5 6 1 2 3 Zerlegungsbeweis Ergänzungsbeweis Nu r z u Pr üf zw ec ke Ei g nt um d es C .C . B uc hn er V rla gs | |
 « |  » |
|
» Zur Flash-Version des Livebooks | |