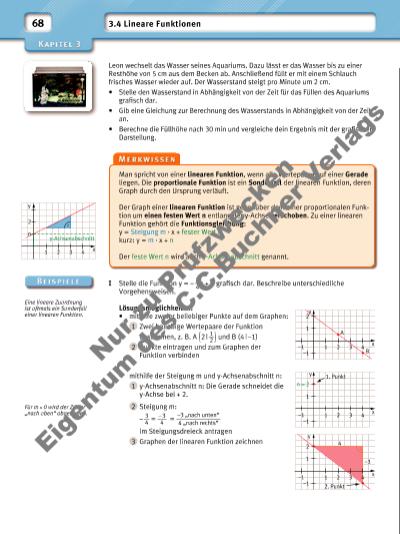
| Volltext anzeigen | |
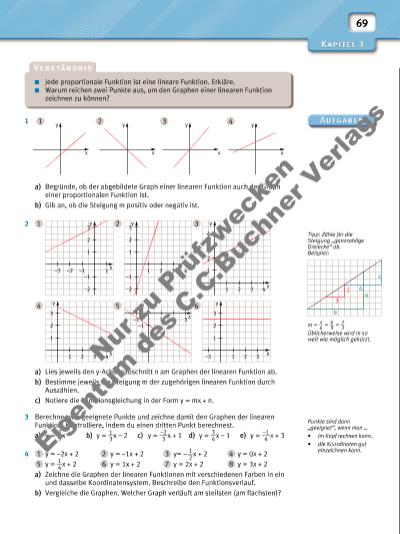
69 Tipp: Zähle für die Steigung „ganzzahlige Dreiecke“ ab. Beispiel: m = 4 __ 6 = 6 __ 9 = 2 __ 3 Üblicherweise wird m so weit wie möglich gekürzt. Punkte sind dann „geeignet“, wenn man … • im Kopf rechnen kann. • die Koordinaten gut einzeichnen kann. 1 a) Begründe, ob der abgebildete Graph einer linearen Funktion auch der Graph einer proportionalen Funktion ist. b) Gib an, ob die Steigung m positiv oder negativ ist. 2 1 2 3 4 5 6 a) Lies jeweils den y-Achsenabschnitt n am Graphen der linearen Funktion ab. b) Bestimme jeweils die Steigung m der zugehörigen linearen Funktion durch Auszählen. c) Notiere die Funktionsgleichung in der Form y = mx + n. 3 Berechne zwei geeignete Punkte und zeichne damit den Graphen der linearen Funktion. Kontrolliere, indem du einen dritten Punkt berechnest. a) y = 2 __ 5 x b) y = 1 __ 3 x – 2 c) y = –2 ___ 3 x + 1 d) y = 3 __ 4 x – 1 e) y = –1 ___ 4 x + 3 4 1 y = –2x + 2 2 y = –1x + 2 3 y= – 1 __ 2 x + 2 4 y = 0x + 2 5 y = 1 __ 4 x + 2 6 y = 1x + 2 7 y = 2x + 2 8 y = 3x + 2 a) Zeichne die Graphen der linearen Funktionen mit verschiedenen Farben in ein und dasselbe Koordinatensystem. Beschreibe den Funktionsverlauf. b) Vergleiche die Graphen. Welcher Graph verläuft am steilsten (am fl achsten)? Jede proportionale Funktion ist eine lineare Funktion. Erkläre. Warum reichen zwei Punkte aus, um den Graphen einer linearen Funktion zeichnen zu können? x y x y x y x y1 2 3 4 1 3 y x 1 2 –1–2–3 –1 –2 4 3 y x 1 2 321 –1 –2 3 y x –2 –3 –1 21–1 4 3 y x 4 1 2 321 3 y x 1 2 321–14 3 y x 1 2 321 4 9 6 3 2 6 Nu r z u Pr üf zw ec ke n Ei g nt um d es C .C .B uc hn er V er la gs | |
 « |  » |
|
» Zur Flash-Version des Livebooks | |