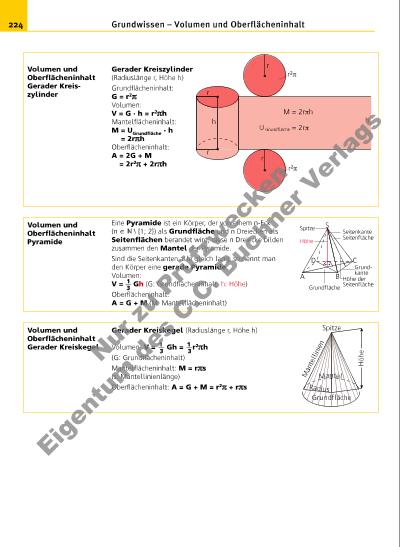
225 Grundwissen – Trigonometrie am rechtwinkligen Dreieck; griechisches Alphabet Α α Alpha Β β Beta Γ γ Gamma δ Delta Ε ε Epsilon Ζ ζ Zeta Η η Eta Θ θ Theta Ι ι Jota Κ κ Kappa Λ λ Lambda Μ My Ν ν Ny Ξ ξ Xi Ο ο Omikron Π π Pi Ρ ρ Rho Σ σ Sigma Τ τ Tau Υ υ Ypsilon Φ Phi Χ χ Chi Ψ ψ Psi ω Omega Griechisches Alphabet Zwischen den Werten des Sinus, des Kosinus und des Tangens spitzer Winkel bestehen Zusammenhänge: Wegen β = 90° – α ist cos α = sin (90°– α) und sin α = cos (90°– α) (sin α)2 + (cos α)2 = 1 tan α = sin _____cos Für die Grenzfälle setzt man fest: sin 0° = cos 90° = 0; sin 90° = cos 0° = 1; tan 0° = 0 Beziehungen zwischen Sinus, Kosinus und Tangens Besondere Winkel 0° 30° 45° 60° 90° sin 0 = 1 __ 2 √ __ 0 1 __ 2 = 1 __ 2 √ __ 1 1 __ 2 √ __ 2 = 1 __ 2 √ __ 2 1 __ 2 √ __ 3 = 1 __ 2 √ __ 3 1 = 1 __ 2 √ __ 4 cos 1 1 __ 2 √ __ 3 1 __ 2 √ __ 2 1 __ 2 0 tan 0 1 __ 3 √ __ 3 1 √ __ 3 – Tangens eines Winkels = Länge der Gegenkathete des Winkels __________________________________ Länge der Ankathete des Winkels Sinus eines Winkels = Länge der Gegenkathete des Winkels __________________________________ Länge der Hypotenuse Kosinus eines Winkels = Länge der Ankathete des Winkels _______________________________ Länge der Hypotenuse tan α = a __ b tan β = b __ a sin α = a __ c sin β = b __ c cos α = b __ c cos β = a __ c Tangens eines Winkels Sinus eines Winkels Kosinus eines Winkels A B C α β b a c Hypotenuse G eg en ka th et e vo n β An ka th et e vo n α Gegenkathete von α Ankathete von β Nu r z u Pr üf zw ec ke n Ei ge n um d es C .C . B uc hn er V rla gs