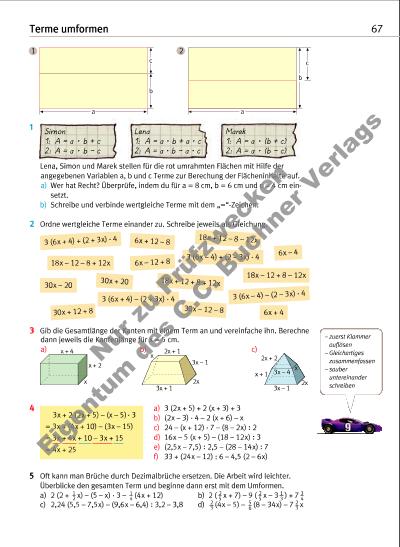
ac b a c b x + 4 x + 2 x 2x + 1 3x – 1 3x + 1 3x – 1 3x – 4 2x + 2 x + 1 x 2x x 2x Terme umformen 67 1 Lena, Simon und Marek stellen für die rot umrahmten Flächen mit Hilfe der angegebenen Variablen a, b und c Terme zur Berechung der Flächeninhalte auf. a) Wer hat Recht? Überprüfe, indem du für a = 8 cm, b = 6 cm und c = 4 cm einsetzt. b) Schreibe und verbinde wertgleiche Terme mit dem „=“-Zeichen. 2 Ordne wertgleiche Terme einander zu. Schreibe jeweils als Gleichung. 3x + 2 (2x + 5) – (x – 5) · 3 = 3x + (4x + 10) – (3x – 15) = 3x + 4x + 10 – 3x + 15 = 4x + 25 4 a) 3 (2x + 5) + 2 (x + 3) + 3 b) (2x – 3) · 4 – 2 (x + 6) – x c) 24 – (x + 12) · 7 – (8 – 2x) ÷ 2 d) 16x – 5 (x + 5) – (18 – 12x) ÷ 3 e) (2,5x – 7,5) ÷ 2,5 – (28 – 14x) ÷ 7 f) 33 + (24x – 12) : 6 – 4,5 (2 – 6x) 5 Oft kann man Brüche durch Dezimalbrüche ersetzen. Die Arbeit wird leichter. Überblicke den gesamten Term und beginne dann erst mit dem Umformen. a) 2 (2 + x) – (5 – x) · 3 – (4x + 12) b) 2 ( x + 7) – 9 ( x – 3 ) + 712 1 4 2 5 2 5 1 3 3 4 c) 2,24 (5,5 – 7,5x) – (9,6x – 6,4) ÷ 3,2 – 3,8 d) (4x – 5) – (8 – 34x) – 7 x23 5 6 2 3 Simon 1: A = a • b + c 2: A = a • b – c Lena 1: A = a • b + a • c 2: A = a • b – a • c Marek 1: A = a • (b + c) 2: A = a • (b – c) 3 Gib die Gesamtlänge der Kanten mit einem Term an und vereinfache ihn. Berechne dann jeweils die Kantenlänge für x = 5 cm. a) b) c) – zuerst Klammer auflösen – Gleichartiges zusammenfassen – sauber unterei n ander schreiben 3 (6x + 4) + (2 + 3x) · 4 3 (6x – 4) – (2 – 3x) · 43 (6x + 4) – (2 + 3x) · 4 3 (6x – 4) + (2 – 3x) · 4 18x – 12 – 8 + 12x 18x + 12 – 8 – 12x 18x + 12 + 8 + 12x 18x – 12 + 8 – 12x 6x – 12 + 8 30x – 12 – 8 6x + 12 – 8 30x + 12 + 8 30x – 20 30x + 20 6x – 4 6x + 4 1 2 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs