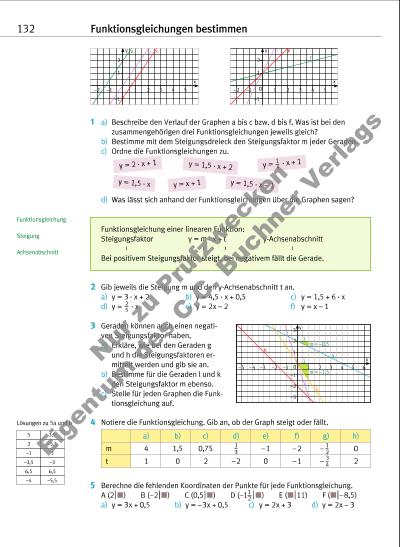
Ursprungsgerade: Gerade, die durch Punkt (0B0) verläuft. Funktionsgleichungen bestimmen 133 1 Lies aus dem Schaubild jeweils den y-Achsenabschnitt t und die Steigung m der Geraden ab und stelle damit die Funktionsgleichung auf. 5 Zeichne eine Ursprungsgerade, die durch den angegebenen Punkt verläuft. Ermittle die jeweilige Steigung und gib die Funktionsgleichung an. a) A (3 B3) b) B (4 B2) c) C (2,5 B7,5) d) D (2 B–2) e) E (–4 B–1) 6 Zeichne die Gerade und gib die Funktionsgleichung an. a) b) c) d) e) f) 7 Zeichne die Gerade AB und bestimme ihre Funktions gleichung. a) A (2 B1) B (6 B3) b) A (–2 B–4) B (3 B6) c) A (1B0) B (5 B8) d) A (–2 B4,5) B (2 B–1,5) e) A (–5 B3) B (5 B2) f) A (–4 B–2) B (8 B–2) 2 Die Ursprungsgerade a hat die Steigung 0,5. Alle übrigen Geraden verlaufen parallel zu a. a) Gib die Funktionsgleichung von a an. b) Stelle die Funktionsgleichungen der anderen vier Geraden auf. 3 a) Lies den Schnittpunkt jeder Geraden mit der y-Achse ab. b) Bestimme die Steigung der jewei ligen Geraden. c) Stelle für jede Gerade die Funk tionsgleichung auf. 4 Eine Gerade verläuft durch P (0 B–3) und schneidet die x-Achse im Punkt Q (6 B0). Gib die zugehörige Funk tionsgleichung an. 1 3 4 5 x 2 1 2 3 y 1 2 t A 0 0 –2 1 2 x –1 1 2 3 y –1 0 –2 1 2 x –1 1 2 y –1–2 1 3 4 5 2 y 0 x 1 2 3–1 B C D g h l k i 2 x y –2 2 4–4 –4 6–2 0 4 b c e d a 2 x y –2 2 –2 4–4 –4 6 4 6 –6 8–6–8 9 10–9–10 Lösungen zu 6 und 7 y = –x – 2 y = 2x – 2 y = – 2 y = 2,5x y = –1,5x + 1,5 y = 1,5x + 1,5 y = – x + 2,5 y = 2x y = 0,5x y = 3x – 1,5 y = – x y = x 1 10 3 4 1 3 x –2 –1 0 1 2 y –5 –2,5 0 2,5 5 x –2 –1 0 1 2 y –1,5 0 1,5 3 4,5 x –6 –3 3 6 9 y 2 1 –1 –2 –3 x –4 0 2 6 y –3 0 1,5 4,5 x –5 –2 1 3 y 3 0 –3 –5 x –2 –1 1 2 3 y –7,5 –4,5 1,5 4,5 7,5 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs