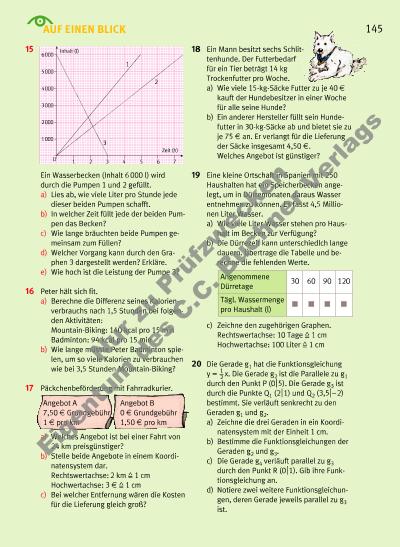
AUF EINEN BLICK 145 15 Ein Wasserbecken (Inhalt 6 000 l) wird durch die Pumpen 1 und 2 gefüllt. a) Lies ab, wie viele Liter pro Stunde jede dieser beiden Pumpen schafft. b) In welcher Zeit füllt jede der beiden Pumpen das Becken? c) Wie lange bräuchten beide Pumpen gemeinsam zum Füllen? d) Welcher Vorgang kann durch den Graphen 3 dargestellt werden? Erkläre. e) Wie hoch ist die Leistung der Pumpe 3? 16 Peter hält sich fit. a) Berechne die Differenz seines Kalorienverbrauchs nach 1,5 Stunden bei folgenden Aktivitäten: Mountain-Biking: 140 kcal pro 15 min Badminton: 94 kcal pro 15 min b) Wie lange müsste Peter Badminton spielen, um so viele Kalorien zu verbrauchen wie bei 3,5 Stunden Mountain-Biking? 17 Päckchenbeförderung mit Fahrradkurier. a) Welches Angebot ist bei einer Fahrt von 24 km preisgünstiger? b) Stelle beide Angebote in einem Koordinatensystem dar. Rechtswertachse: 2 km q 1 cm Hochwertachse: 3 “ q 1 cm c) Bei welcher Entfernung wären die Kosten für die Lieferung gleich groß? 2000 1 3000 2 3 4 Inhalt (l) 1000 4000 5 6 7 5000 6000 Zeit (h) 1 2 3 0 Angenommene 30 60 90 120 Dürretage Tägl. Wassermenge M M M M pro Haushalt (l) Angebot A 7,50 “ Grundgebühr 1 “ pro km Angebot B 0 “ Grundgebühr 1,50 “ pro km 18 Ein Mann besitzt sechs Schlittenhunde. Der Futterbedarf für ein Tier beträgt 14 kg Trockenfutter pro Woche. a) Wie viele 15-kg-Säcke Futter zu je 40 “ kauft der Hundebesitzer in einer Woche für alle seine Hunde? b) Ein anderer Hersteller füllt sein Hundefutter in 30-kg-Säcke ab und bietet sie zu je 75 “ an. Er verlangt für die Lieferung der Säcke insgesamt 4,50 “. Welches Angebot ist günstiger? 19 Eine kleine Ortschaft in Spanien mit 250 Haushalten hat ein Speicherbecken angelegt, um in Dürremonaten daraus Wasser entnehmen zu können. Es fasst 4,5 Millionen Liter Wasser. a) Wie viele Liter Wasser stehen pro Haushalt im Becken zur Verfügung? b) Die Dürrezeit kann unterschiedlch lange dauern. Übertrage die Tabelle und berechne die fehlenden Werte. c) Zeichne den zugehörigen Graphen. Rechtswertachse: 10 Tage q 1 cm Hochwertachse: 100 Liter q 1 cm 20 Die Gerade g1 hat die Funktionsgleichung y = x. Die Gerade g2 ist die Parallele zu g1 durch den Punkt P (0 B5). Die Gerade g3 ist durch die Punkte Q1 (2 B1) und Q2 (3,5 B–2) bestimmt. Sie verläuft senkrecht zu den Geraden g1 und g2. a) Zeichne die drei Geraden in ein Koordinatensystem mit der Einheit 1 cm. b) Bestimme die Funktionsgleichungen der Geraden g2 und g3. c) Die Gerade g4 verläuft parallel zu g3 durch den Punkt R (0 B1). Gib ihre Funk tionsgleichung an. d) Notiere zwei weitere Funktionsgleichungen, deren Gerade jeweils parallel zu g3 ist. 1 2 Nu r z u Pr üf zw ec en Ei ge nt um d es C .C . B uc hn er V er la gs