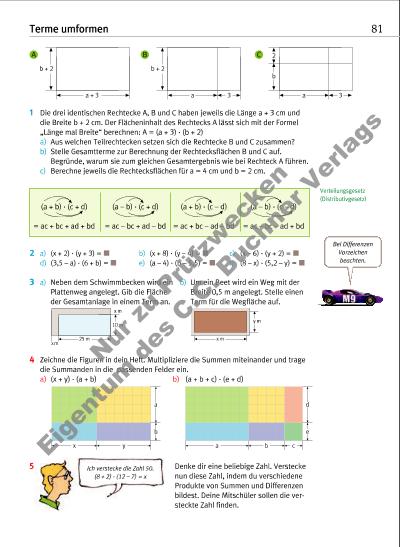
x y a b a b c d e Bei Differenzen Vorzeichen beachten. Terme umformen 81 1 Die drei identischen Rechtecke A, B und C haben jeweils die Länge a + 3 cm und die Breite b + 2 cm. Der Flächeninhalt des Rechtecks A lässt sich mit der Formel „Länge mal Breite“ berechnen: A = (a + 3) · (b + 2) a) Aus welchen Teilrechtecken setzen sich die Rechtecke B und C zusammen? b) Stelle Gesamtterme zur Berechnung der Rechtecksflächen B und C auf. Begründe, warum sie zum gleichen Gesamtergebnis wie bei Rechteck A führen. c) Berechne jeweils die Rechtecksflächen für a = 4 cm und b = 2 cm. b + 2 a + 3 b + 2 a 3 b a 3 2 2 a) (x + 2) · (y + 3) = M b) (x + 8) · (y – 4) = M c) (x – 6) · (y + 2) = M d) (3,5 – a) · (6 + b) = M e) (a – 4) · (b – 5,5) = M f) (8 – x) · (5,2 – y) = M 3 4 Zeichne die Figuren in dein Heft. Multipliziere die Summen miteinander und trage die Summanden in die passenden Felder ein. a) (x + y) · (a + b) b) (a + b + c) · (e + d) 5 x m y m 25 m 10 m x m x m a) Neben dem Schwimmbecken wird ein Plattenweg angelegt. Gib die Fläche der Gesamtanlage in einem Term an. b) Um ein Beet wird ein Weg mit der Breite 0,5 m angelegt. Stelle einen Term für die Wegfläche auf. (a + b) · (c + d) (a – b) · (c + d) (a + b) · (c – d) (a – b) · (c – d) = ac + bc + ad + bd = ac – bc + ad – bd = ac + bc – ad – bd = ac – bc – ad + bd Verteilungsgesetz (Distributivgesetz) Denke dir eine beliebige Zahl. Verstecke nun diese Zahl, indem du verschiedene Produkte von Summen und Differenzen bildest. Deine Mitschüler sollen die versteckte Zahl finden. Ich verstecke die Zahl 50. (8 + 2) · (12 – 7) = x A B C Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs