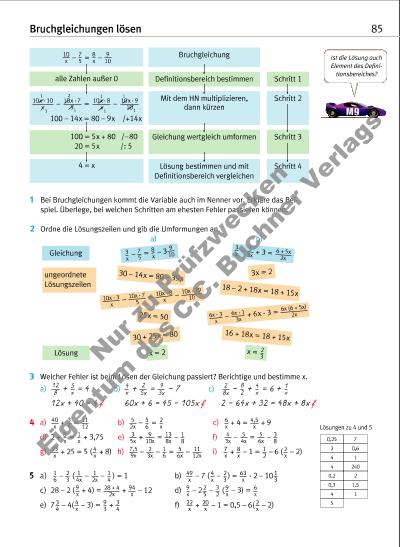
Bruchgleichungen lösen 85 5 a) – ( – – ) = 1 b) – 7 ( – ) = · 2 – 101 6 2 3 1 4x 1 2x 1 4 49 x 63 x 4 x 2 3 1 3 c) 28 – 2 ( + 4) = + – 12 d) – 2 – ( – 3) = 9 x 9 x 2 5 3 2 9 x 6 x 28 + 4 2x 94 x e) 7 – 4( – 3) = + f) + – 1 = 0,5 – 6( – 2)3 4 2 x 4 x 9 3 3 4 22 x 20 x 1 Bei Bruchgleichungen kommt die Variable auch im Nenner vor. Erkläre das Beispiel. Überlege, bei welchen Schritten am ehesten Fehler passieren können. 2 Ordne die Lösungszeilen und gib die Umformungen an. Gleichung ungeordnete Lösungszeilen Lösung 30 – 14x = 80 – 39x 25x = 50 x = 2 – = – 33 x 8 x 7 5 9 10 – = – 10x · 3 x 10x · 7 5 10x · 8 x 10x · 39 10 a) b) 3x = 2 18 – 2 + 18x = 18 + 15x x = 2 3 – + 3 = 3 x 1 3x 6 + 5x 2x – + 6x · 3 = 6x · 3 x 6x (6 + 5x) 2x6x · 1 3x 30 + 25x = 80 16 + 18x = 18 + 15x 3 Welcher Fehler ist beim Lösen der Gleichung passiert? Berichtige und bestimme x. a) + = 4 b) + = – 7 c) – + = 6 + 128 5 x 4 x 2 5x 9 3x 2 8x 4 x 1 x 8 2 12x + 40 = 4 f 60x + 6 = 45 – 105x f 2 – 64x + 32 = 48x + 8x f 4 a) + = b) – = c) + 4 = + 940 x 3 4 11 12 5 2x 5 6 2 x 6 x 4,5 x d) 2 + = + 3,75 e) + = – f) – = –8 x 3 5x 9 10x 5 6x 1 x 13 8x 1 8 4 3x 5 4x 3 8 g) + 25 = 5 ( + 8) h) – – = – i) + – 1 = – 6 ( – 2)7,5 9x 4 x 5 6x 23 x 2 3x 1 6 11 12x 7 x 8 x 1 2 2 x Lösungen zu 4 und 5 0,25 7 2 0,6 4 1 4 240 0,2 2 0,3 1,5 4 5 1 Ist die Lösung auch Element des Definitionsbereiches? – = – 100 – 14x = 80 – 9x /+14x 100 = 5x + 80 /–80 20 = 5x /÷ 5 4 = x Lösung bestimmen und mit Definitionsbereich vergleichen 10x · 10 x 10x · 7 5 10x · 8 x 10x · 9 10 1 2 1 1 1 1 1 1 – = – 10x 7 5 8 x 9 10 Bruchgleichung Schritt 1 Schritt 2 Schritt 3 Schritt 4 Definitionsbereich bestimmen Mit dem HN multiplizieren, dann kürzen Gleichung wertgleich umformen alle Zahlen außer 0 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs