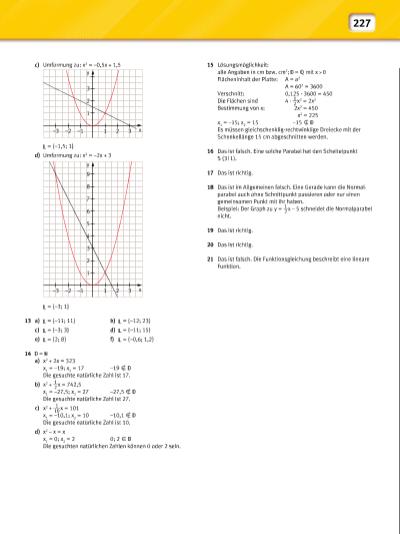
227 c) Umformung zu: x2 = –0,5x + 1,5 = {–1,5; 1} d) Umformung zu: x2 = –2x + 3 = {–3; 1} 13 a) = {–11; 11} b) = {–12; 23} c) = {–3; 3} d) = {–11; 15} e) = {2; 8} f) = {–0,6; 1,2} 14 = a) x2 + 2x = 323 x1 = –19; x2 = 17 –19 x Die gesuchte natürliche Zahl ist 17. b) x2 + 1 __ 2 x = 742,5 x1 = –27,5; x2 = 27 –27,5 x Die gesuchte natürliche Zahl ist 27. c) x2 + 1 ___ 10 x = 101 x1 = –10,1; x2 = 10 –10,1 x Die gesuchte natürliche Zahl ist 10. d) x2 – x = x x1 = 0; x2 = 2 0; 2 X Die gesuchten natürlichen Zahlen können 0 oder 2 sein. 15 Lösungsmöglichkeit: alle Angaben in cm bzw. cm2; = mit x 0 Flächeninhalt der Platte: A = a2 A = 602 = 3600 Verschnitt: 0,125 · 3600 = 450 Die Flächen sind 4 · 1 __ 2 x 2 = 2x2 Bestimmung von x: 2x2 = 450 x2 = 225 x1 = –15; x2 = 15 –15 x Es müssen gleichschenklig-rechtwinklige Dreiecke mit der Schenkellänge 15 cm abgeschnitten werden. 16 Das ist falsch. Eine solche Parabel hat den Scheitelpunkt S (3 | 1). 17 Das ist richtig. 18 Das ist im Allgemeinen falsch. Eine Gerade kann die Normalparabel auch ohne Schnittpunkt passieren oder nur einen gemeinsamen Punkt mit ihr haben. Beispiel: Der Graph zu y = 1 __ 2 x – 5 schneidet die Normalparabel nicht. 19 Das ist richtig. 20 Das ist richtig. 21 Das ist falsch. Die Funktionsgleichung beschreibt eine lineare Funktion. 1 –3 –2 –1 1 2 3 2 3 x y 1 –3 –2 –1 1 2 3 2 3 4 5 6 7 8 9 x y