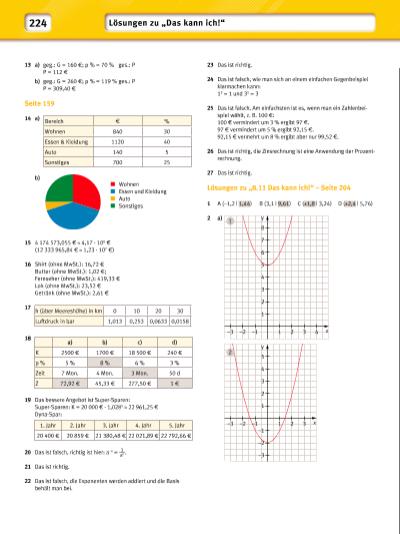
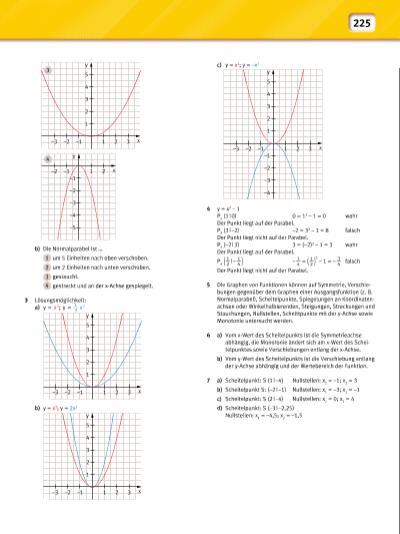
225 b) Die Normalparabel ist … 1 um 5 Einheiten nach oben verschoben. 2 um 2 Einheiten nach unten verschoben. 3 gestaucht. 4 gestreckt und an der x-Achse gespiegelt. 3 Lösungsmöglichkeit: a) y = x2; y = 1 __ 3 x 2 b) y = x2; y = 2x2 1 –3 –2 –1 1 2 3 2 3 4 5 x y –4 –5 –2 –1 1 2 –3 –2 –1 x y 3 4 c) y = x2; y = –x2 4 y = x2 – 1 P1 (1 | 0) 0 = 1 2 – 1 = 0 wahr Der Punkt liegt auf der Parabel. P2 (3 | –2) –2 = 3 2 – 1 = 8 falsch Der Punkt liegt nicht auf der Parabel. P3 (–2 | 3) 3 = (–2) 2 – 1 = 3 wahr Der Punkt liegt auf der Parabel. P4 ( 1 __ 2 | – 1 __ 4 ) – 1 __ 4 = ( 1 __ 2 ) 2 – 1 = – 3 __ 4 falsch Der Punkt liegt nicht auf der Parabel. 5 Die Graphen von Funktionen können auf Symmetrie, Verschiebungen gegenüber dem Graphen einer Ausgangsfunktion (z. B. Normalparabel), Scheitelpunkte, Spiegelungen an Koordinatenachsen oder Winkelhalbierenden, Steigungen, Streckungen und Stauchungen, Nullstellen, Schnittpunkte mit der y-Achse sowie Monotonie untersucht werden. 6 a) Vom x-Wert des Scheitelpunkts ist die Symmetrieachse abhängig, die Monotonie ändert sich am x-Wert des Scheitelpunktes sowie Verschiebungen entlang der x-Achse. b) Vom y-Wert des Scheitelpunkts ist die Verschiebung entlang der y-Achse abhängig und der Wertebereich der Funktion. 7 a) Scheitelpunkt: S (1 | –4) Nullstellen: x1 = –1; x2 = 3 b) Scheitelpunkt S: (–2 | –1) Nullstellen: x1 = –3; x2 = –1 c) Scheitelpunkt: S (2 | –4) Nullstellen: x1 = 0; x2 = 4 d) Scheitelpunkt: S (–3 | –2,25) Nullstellen: x1 = –4,5; x2 = –1,5 1 –3 –2 –1 1 2 3 2 3 4 5 x y 1 –3 –2 –1 1 2 3 2 3 4 5 x y 1 –1 –2 –3 –4 –3 –2 –1 1 2 3 2 3 4 5 x y