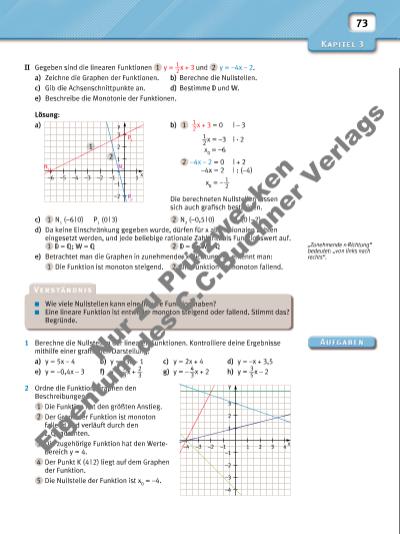
73 II Gegeben sind die linearen Funktionen 1 y = 1 __ 2 x + 3 und 2 y = –4x – 2. a) Zeichne die Graphen der Funktionen. b) Berechne die Nullstellen. c) Gib die Achsenschnittpunkte an. d) Bestimme und . e) Beschreibe die Monotonie der Funktionen. Lösung: a) b) 1 1 __ 2 x + 3 = 0 | – 3 1 __ 2 x = –3 | · 2 x0 = –6 2 –4x – 2 = 0 | + 2 –4x = 2 | : (–4) x0 = – 1 __ 2 Die berechneten Nullstellen lassen sich auch grafi sch bestätigen. c) 1 N1 (–6 | 0) P1 (0 | 3) 2 N2 (–0,5 | 0) P2 (0 | –2) d) Da keine Einschränkung gegeben wurde, dürfen für x alle rationalen Zahlen eingesetzt werden, und jede beliebige rationale Zahl tritt als Funktionswert auf. 1 = ; = 2 = ; = e) Betrachtet man die Graphen in zunehmender x-Richtung, so erkennt man: 1 Die Funktion ist monoton steigend. 2 Die Funktion ist monoton fallend. „Zunehmende x-Richtung“ bedeutet: „von links nach rechts“. 1 Berechne die Nullstellen der linearen Funktionen. Kontrolliere deine Ergebnisse mithilfe einer grafi schen Darstellung. a) y = 5x – 4 b) y = –3x – 1 c) y = 2x + 4 d) y = –x + 3,5 e) y = –0,4x – 3 f) y = 7 __ 3 x + 2 __ 3 g) y = – 4 __ 3 x + 2 h) y = 3 __ 5 x – 2 2 Ordne die Funktionsgraphen den Beschreibungen zu. 1 Die Funktion hat den größten Anstieg. 2 Der Graph der Funktion ist monoton fallend und verläuft durch den I. Quadranten. 3 Die zugehörige Funktion hat den Wertebereich y = 4. 4 Der Punkt K (4 | 2) liegt auf dem Graphen der Funktion. 5 Die Nullstelle der Funktion ist x0 = –4. Wie viele Nullstellen kann eine lineare Funktion haben? Eine lineare Funktion ist entweder monoton steigend oder fallend. Stimmt das? Begründe. 1 2 3 4 3 y x 1 2 –2 –1 –1 –4 –3 –2 –3 –4 1 P 1 P 2 N 2 N 1 3 y x 1 2 –1–2–3–4–5–6 –1 –2 1 2 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs