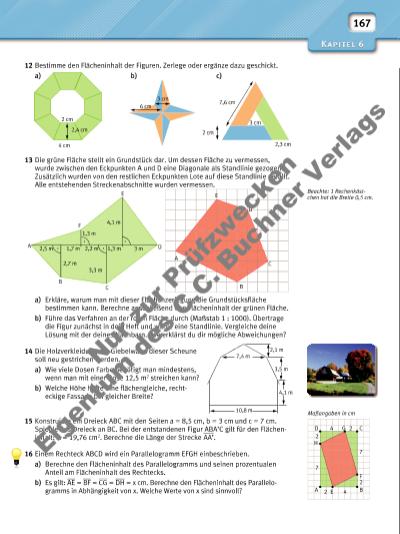
167 2 cm 4 cm 3 cm 6 cm 2,3 cm 2 cm 7,6 cm 3 cm 2,4 cm 10,8 m 7,4 m 3,5 m 4,1 m 2,1 m Maßangaben in cm D G4 42 2 2 7 7 2 H E F C A B A B C D E B C 2,5 m 3 m 3,3 m 2,2 m 2,7 m 4,1 m 1,3 m1,7 m 1,3 m D E F A Beachte: 1 Rechenkästchen hat die Breite 0,5 cm. 12 Bestimme den Flächeninhalt der Figuren. Zerlege oder ergänze dazu geschickt. a) b) c) 13 Die grüne Fläche stellt ein Grundstück dar. Um dessen Fläche zu vermessen, wurde zwischen den Eckpunkten A und D eine Diagonale als Standlinie gezogen. Zusätzlich wurden von den restlichen Eckpunkten Lote auf diese Standlinie gefällt. Alle entstehenden Streckenabschnitte wurden vermessen. a) Erkläre, warum man mit dieser Flächenzerlegung die Grundstücksfl äche bestimmen kann. Berechne anschließend den Flächeninhalt der grünen Fläche. b) Führe das Verfahren an der roten Fläche durch (Maßstab 1 : 1000). Übertrage die Figur zunächst in dein Heft und wähle eine Standlinie. Vergleiche deine Lösung mit der deines Nachbarn. Wie erklärst du dir mögliche Abweichungen? 14 Die Holzverkleidung der Giebelwand dieser Scheune soll neu gestrichen werden. a) Wie viele Dosen Farbe benötigt man mindestens, wenn man mit einer Dose 12,5 m2 streichen kann? b) Welche Höhe hätte eine fl ächengleiche, rechteckige Fassade bei gleicher Breite? 15 Konstruiere ein Dreieck ABC mit den Seiten a = 8,5 cm, b = 3 cm und c = 7 cm. Spiegle das Dreieck an BC. Bei der entstandenen Figur ABA’C gilt für den Flächeninhalt: A = 19,76 cm2. Berechne die Länge der Strecke ___ AA’. 16 Einem Rechteck ABCD wird ein Parallelogramm EFGH einbeschrieben. a) Berechne den Flächeninhalt des Parallelogramms und seinen prozentualen Anteil am Flächeninhalt des Rechtecks. b) Es gilt: ___ AE = ___ BF = ___ CG = ___ DH = x cm. Berechne den Flächeninhalt des Parallelogramms in Abhängigkeit von x. Welche Werte von x sind sinnvoll? Nu r z ur P rü fzw ec ke n Ei g nt um d es C .C . B uc hn er V er la gs