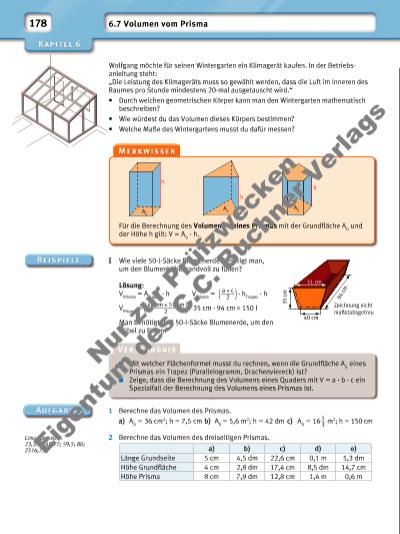
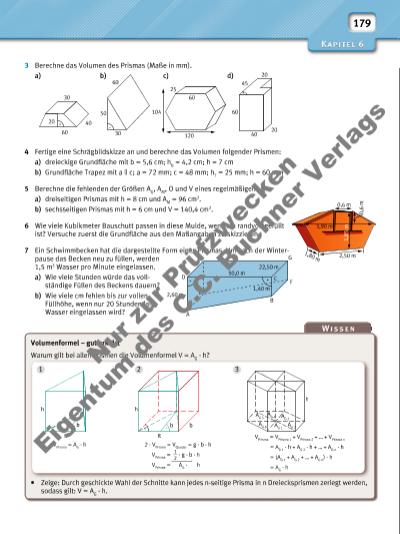
179 1 2 3 h A G 1 A G 2 A G 3 A G 4AG 5 A G 6 h bb g h b g 3 Berechne das Volumen des Prismas (Maße in mm). a) b) c) d) 4 Fertige eine Schrägbildskizze an und berechne das Volumen folgender Prismen: a) dreieckige Grundfl äche mit b = 5,6 cm; hb = 4,2 cm; h = 7 cm b) Grundfl äche Trapez mit a || c; a = 72 mm; c = 48 mm; hT = 25 mm; h = 60 mm 5 Berechne die fehlenden der Größen AG, AM, O und V eines regelmäßigen … a) dreiseitigen Prismas mit h = 8 cm und AM = 96 cm 2. b) sechsseitigen Prismas mit h = 6 cm und V = 140,4 cm2. 6 Wie viele Kubikmeter Bauschutt passen in diese Mulde, wenn sie randvoll gefüllt ist? Versuche zuerst die Grundfl äche aus den Maßangaben zu skizzieren. 7 Ein Schwimmbecken hat die dargestellte Form eines Prismas. Um nach der Winterpause das Becken neu zu füllen, werden 1,5 m3 Wasser pro Minute eingelassen. a) Wie viele Stunden würde das vollständige Füllen des Beckens dauern? b) Wie viele cm fehlen bis zur vollen Füllhöhe, wenn nur 20 Stunden lang Wasser eingelassen wird? Volumenformel – gut erklärt Warum gilt bei allen Prismen die Volumenformel V = AG · h? • Zeige: Durch geschickte Wahl der Schnitte kann jedes n-seitige Prisma in n Dreiecksprismen zerlegt werden, sodass gilt: V = AG · h. 60 30 120 40 104 60 20 50 30 60 25 60 45 20 20 40 2,50 m 0,6 m 3,90 m 1,80 m 1, 85 m 0, 6 m VPrisma = AG · h VPrisma = VPrisma 1 + VPrisma 2 + … + VPrisma n = AG 1 · h + AG 2 · h + … + AG n · h = (AG 1 + AG 2 + … + AG n) · h = AG · h 2 · VPrisma = VQuader = g · b · h VPrisma = 1 __ 2 · g · b · h VPrisma = AG · h A 2,60 m 1,40 m 50,0 m 22,50 m B F E H G CD Nu r z ur P rü fzw ec ke n Ei en tu m d es C .C . B uc hn er V er la gs