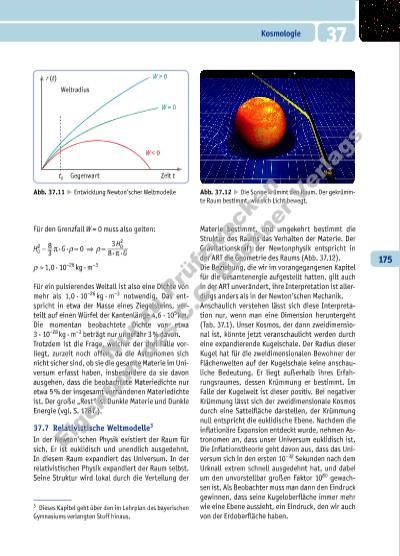
175 37Kosmologie Für den Grenzfall W = 0 muss also gelten: H0 2 − pi · G ·ρ = 0 ⇒ ρ = 3H0 2 8 · pi · G 8 3 ρ ≈ 1,0 · 10–26 kg · m–3 Für ein pulsierendes Weltall ist also eine Dichte von mehr als 1,0 · 10–26 kg · m–3 notwendig. Das entspricht in etwa der Masse eines Ziegelsteins, verteilt auf einen Würfel der Kantenlänge 4,6 · 105 km. Die momentan beobachtete Dichte von etwa 3 · 10–28 kg · m–3 beträgt nur ungefähr 3 % davon. Trotzdem ist die Frage, welcher der drei Fälle vorliegt, zurzeit noch offen, da die Astronomen sich nicht sicher sind, ob sie die gesamte Materie im Universum erfasst haben, insbesondere da sie davon ausgehen, dass die beobachtete Materiedichte nur etwa 5 % der insgesamt vorhandenen Materiedichte ist. Der große „Rest“ ist Dunkle Materie und Dunkle Energie (vgl. S. 178 f.). 37.7 Relativistische Weltmodelle3 In der Newton’schen Physik existiert der Raum für sich. Er ist euklidisch und unendlich ausgedehnt. In diesem Raum expandiert das Universum. In der relativistischen Physik expandiert der Raum selbst. Seine Struktur wird lokal durch die Verteilung der 3 Dieses Kapitel geht über den im Lehrplan des bayerischen Gymnasiums verlangten Stoff hinaus. Abb. 37.11 E Entwicklung Newton’scher Weltmodelle Abb. 37.12 E Die Sonne krümmt den Raum. Der gekrümmte Raum bestimmt, wie sich Licht bewegt. r (t) Weltradius Zeit t W > 0 W = 0 W < 0 Gegenwartt0 Materie bestimmt, und umgekehrt bestimmt die Struktur des Raums das Verhalten der Materie. Der Gravitationskraft der Newtonphysik entspricht in der ART die Geometrie des Raums (Abb. 37.12). Die Beziehung, die wir im vorangegangenen Kapitel für die Gesamtenergie aufgestellt hatten, gilt auch in der ART unverändert, ihre Interpretation ist allerdings anders als in der Newton’schen Mechanik. Anschaulich verstehen lässt sich diese Interpretation nur, wenn man eine Dimension heruntergeht (Tab. 37.1). Unser Kosmos, der dann zweidimensional ist, könnte jetzt veranschaulicht werden durch eine expandierende Kugelschale. Der Radius dieser Kugel hat für die zweidimensionalen Bewohner der Flächenwelten auf der Kugelschale keine anschauliche Bedeutung. Er liegt außerhalb ihres Erfahrungsraumes, dessen Krümmung er bestimmt. Im Falle der Kugelwelt ist dieser positiv. Bei negativer Krümmung lässt sich der zweidimensionale Kosmos durch eine Sattelläche darstellen, der Krümmung null entspricht die euklidische Ebene. Nachdem die inlationäre Expansion entdeckt wurde, nehmen Astronomen an, dass unser Universum euklidisch ist. Die Inlationstheorie geht davon aus, dass das Universum sich in den ersten 10–32 Sekunden nach dem Urknall extrem schnell ausgedehnt hat, und dabei um den unvorstellbar großen Faktor 1080 gewachsen ist. Als Beobachter muss man dann den Eindruck gewinnen, dass seine Kugeloberläche immer mehr wie eine Ebene aussieht, ein Eindruck, den wir auch von der Erdoberläche haben. N u r zu P rü fz w c k e n E ig e n tu m d e s C .C . B u c h n e r V e rl a g s