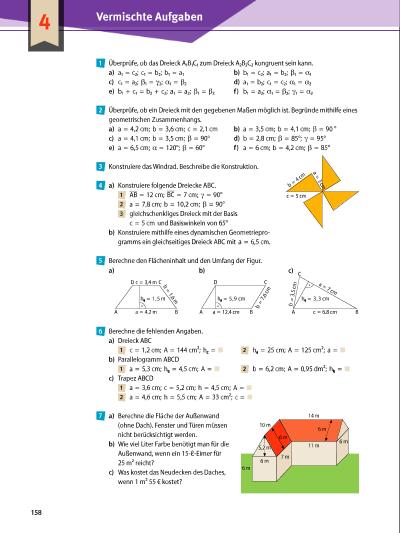
Überprüfe, ob das Dreieck A1B1C1 zum Dreieck A2B2C2 kongruent sein kann. a) a1 = c2; c1 = b2; b1 = a1 b) b1 = c2; a1 = b2; β1 = α1 c) c1 = a2; β1 = γ2; α1 = β2 d) a1 = b2; c1 = c2; α1 = α2 e) b1 + c1 = b2 + c2; a1 = a2; β1 = β2 f) b1 = a2; α1 = β2; γ1 = α2 Überprüfe, ob ein Dreieck mit den gegebenen Maßen möglich ist. Begründe mithilfe eines geometrischen Zusammenhangs. a) a = 4,2 cm; b = 3,6 cm; c = 2,1 cm b) a = 3,5 cm; b = 4,1 cm; β = 90 ° c) a = 4,1 cm; b = 3,5 cm; β = 90° d) b = 2,8 cm; β = 85°; γ = 95° e) a = 6,5 cm; α = 120°; β = 60° f) a = 6 cm; b = 4,2 cm; β = 85° Konstruiere das Windrad. Beschreibe die Konstruktion. a) Konstruiere folgende Dreiecke ABC. 1 ___ AB = 12 cm; ___ BC = 7 cm; γ = 90° 2 a = 7,8 cm; b = 10,2 cm; β = 90° 3 gleichschenkliges Dreieck mit der Basis c = 5 cm und Basiswinkeln von 65° b) Konstruiere mithilfe eines dynamischen Geometriepro­ gramms ein gleich seitiges Dreieck ABC mit a = 6,5 cm. Berechne den Flächeninhalt und den Umfang der Figur. Berechne die fehlenden Angaben. a) Dreieck ABC 1 c = 1,2 cm; A = 144 cm2; hc = ■ 2 ha = 25 cm; A = 125 cm2; a = ■ b) Parallelogramm ABCD 1 a = 5,3 cm; ha = 4,5 cm; A = ■ 2 b = 6,2 cm; A = 0,95 dm2; hb = ■ c) Trapez ABCD 1 a = 3,6 cm; c = 5,2 cm; h = 4,5 cm; A = ■ 2 a = 4,6 cm; h = 5,5 cm; A = 33 cm2; c = ■ a) Berechne die Fläche der Außenwand (ohne Dach). Fenster und Türen müssen nicht berücksichtigt werden. b) Wie viel Liter Farbe benötigt man für die Außenwand, wenn ein 15­ℓ­Eimer für 25 m2 reicht? c) Was kostet das Neudecken des Daches,  wenn 1 m2 55 € kostet? 1 2 3 b = 4 cm a = 3 cm c = 5 cm 4 5 a) b) c) A B A D C B BA C CD a = 4,2 m a = 12,4 cm c = 6,8 cm b = 3 ,5 c m a = 7 cm c = 3,4 m b = 1,6 m b = 7, 6 cm ha = 1,5 m ha = 5,9 cm ha = 3,3 cm 6 6 m 10 m 6 m 6 m 6 m 5,2 m 6 m 7 m 11 m 14 m7 4 Vermischte Aufgaben 158