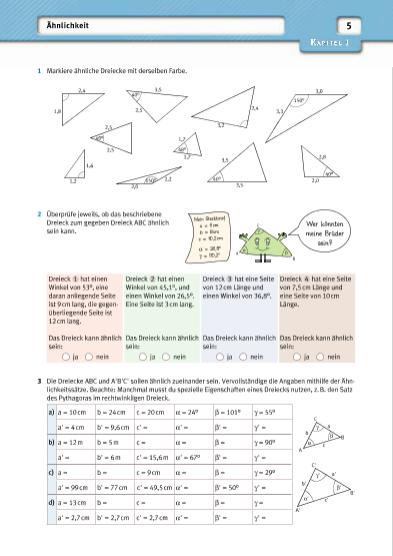
5Kapitel 1 Ähnlichkeit 1 Markiere ähnliche Dreiecke mit derselben Farbe. 2,4 1,8 2,4 3,2 1,6 1,2 40° 2,5 2,5 40° 3,5 2,5 48° 1,7 1,7 150° 3,0 3,3 150° 2,0 2,2 40° 3,5 3,5 40° 2,0 2,8 2 Überprüfe jeweils, ob das beschriebene Wer könnten meine Brüder sein? γ βαA B C Mein Steckbrief a = 6 cm b = 8 cm c = 10,2 cm α = 36,8° γ = 90,2° Dreieck zum gegeben Dreieck ABC ähnlich sein kann. Dreieck 1 hat einen Winkel von 53°, eine daran anliegende Seite ist 9 cm lang, die gegenüberliegende Seite ist 12 cm lang. Das Dreieck kann ähnlich sein: ja nein Dreieck 2 hat einen Winkel von 45,1°, und einen Winkel von 26,5°. Eine Seite ist 3 cm lang. Das Dreieck kann ähnlich sein: ja nein Dreieck 3 hat eine Seite von 12 cm Länge und einen Winkel von 36,8°. Das Dreieck kann ähnlich sein: ja nein Dreieck 4 hat eine Seite von 7,5 cm Länge und eine Seite von 10 cm Länge. Das Dreieck kann ähnlich sein: ja nein 3 Die Dreiecke ABC und A'B'C' sollen ähnlich zueinander sein. Vervollständige die Angaben mithilfe der Ähnlichkeitssätze. Beachte: Manchmal musst du spezielle Eigenschaften eines Dreiecks nutzen, z. B. den Satz des Pythagoras im rechtwinkligen Dreieck. a) a = 10 cm b = 24 cm c = 20 cm α = 24° β = 101° γ = 55° A' a' α' B' b' β' C' c' γ' A a α B b β C c γa' = 4 cm b' = 9,6 cm c' = α' = β' = γ ' = b) a = 12 m b = 5 m c = α = β = γ = 90° a' = b' = 6 m c' = 15,6 m α' = 67° β' = γ ' = c) a = b = c = 9 cm α = β = γ = 29° a' = 99 cm b' = 77 cm c' = 49,5 cm α' = β' = 50° γ ' = d) a = 13 cm b = c = α = β = γ = a' = 2,7 cm b' = 2,7 cm c' = 2,7 cm α' = β' = γ ' =