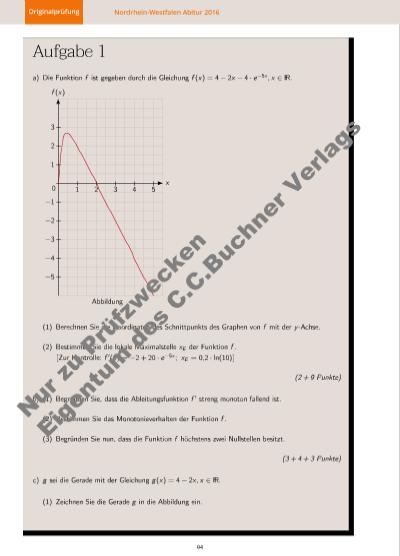
Originalprüfung Nordrhein-Westfalen Abitur 2016 Aufgabe 1 a) Die Funktion f ist gegeben durch die Gleichung f (x) = 4− 2x − 4 · e−5x , x ∈ R . 1 2 3 4 50 −5 −4 −3 −2 −1 1 2 3 f (x) x Abbildung (1) Berechnen Sie die Koordinaten des Schnittpunkts des Graphen von f mit der y -Achse. (2) Bestimmen Sie die lokale Maximalstelle xE der Funktion f .[ Zur Kontrolle: f ′(x) = −2 + 20 · e−5x ; xE = 0,2 · ln(10) ] (2 + 9 Punkte) b) (1) Begründen Sie, dass die Ableitungsfunktion f ′ streng monoton fallend ist. (2) Bestimmen Sie das Monotonieverhalten der Funktion f . (3) Begründen Sie nun, dass die Funktion f höchstens zwei Nullstellen besitzt. (3 + 4 + 3 Punkte) c) g sei die Gerade mit der Gleichung g(x) = 4− 2x , x ∈ R . (1) Zeichnen Sie die Gerade g in die Abbildung ein. 94 Nu r z u Pr üf zw ec ke n Ei ge tu m d e C .C .B uc hn er V er la gs