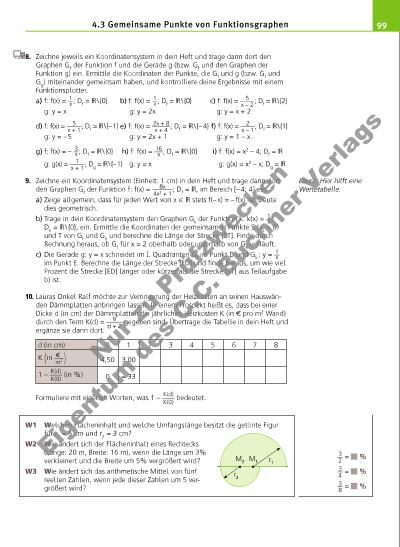
99 8. Zeichne jeweils ein Koordinatensystem in dein Heft und trage dann dort den Graphen Gf der Funktion f und die Gerade g (bzw. Gf und den Graphen der Funktion g) ein. Ermittle die Koordinaten der Punkte, die Gf und g (bzw. Gf und Gg) miteinander gemeinsam haben, und kontrolliere deine Ergebnisse mit einem Funktionsplotter. a) f: f(x) = 1 __ x ; Df = \ {0} b) f: f(x) = 1 __ x ; Df = \ {0} c) f: f(x) = 5 _____ x – 2 ; Df = \ {2} g: y = x g: y = 2x g: y = x + 2 d) f: f(x) = 5 _____ x + 1 ; Df = \ {– 1} e) f: f(x) = 2x + 8 ______ x + 4 ; Df = \ {– 4} f) f: f(x) = 2 _____ x – 1 ; Df = \ {1} g: y = – 5 g: y = 2x + 1 g: y = 1 – x g) f: f(x) = – 3 __ x ; Df = \ {0} h) f: f(x) = 16 ___ x ; Df = \ {0} i) f: f(x) = x 2 – 4; Df = g: g(x) = 1 _____ x + 1 ; Dg = \ {– 1} g: y = x g: g(x) = x 2 – x; Dg = 9. Zeichne ein Koordinatensystem (Einheit: 1 cm) in dein Heft und trage dann dort den Graphen Gf der Funktion f: f(x) = 8x ______ 4x2 + 1 ; Df = , im Bereich [– 4; 4] ein. a) Zeige allgemein, dass für jeden Wert von x X stets f(– x) = – f(x) ist. Deute dies geometrisch. b) Trage in dein Koordinatensystem den Graphen Gk der Funktion k: k(x) = 1 __ x ; Dk = \ {0}, ein. Ermittle die Koordinaten der gemeinsamen Punkte S (xS > 0) und T von Gf und Gk und berechne die Länge der Strecke [ST]. Finde durch Rechnung heraus, ob Gf für x = 2 oberhalb oder unterhalb von Gk verläuft. c) Die Gerade g: y = x schneidet im I. Quadranten Gf im Punkt D und Gk : y = 1 __ x im Punkt E. Berechne die Länge der Strecke [ED] und fi nde heraus, um wie viel Prozent die Strecke [ED] länger oder kürzer als die Strecke [ST] aus Teilaufgabe b) ist. 10. Lauras Onkel Ralf möchte zur Verringerung der Heizkosten an seinen Hauswänden Dämmplatten anbringen lassen. In einem Prospekt heißt es, dass bei einer Dicke d (in cm) der Dämmplatten die jährlichen Heizkosten K (in f pro m2 Wand) durch den Term K(d) = 9 _____ d + 2 gegeben sind. Übertrage die Tabelle in dein Heft und ergänze sie dann dort. Formuliere mit eigenen Worten, was 1 – K(d) ____ K(0) bedeutet. W1 Welchen Flächeninhalt und welche Umfangslänge besitzt die getönte Figur für r1 = 5 cm und r2 = 3 cm? W2 Wie ändert sich der Flächeninhalt eines Rechtecks (Länge: 20 m, Breite: 16 m), wenn die Länge um 3% verkleinert und die Breite um 5% vergrößert wird? W3 Wie ändert sich das arithmetische Mittel von fünf reellen Zahlen, wenn jede dieser Zahlen um 5 vergrößert wird? Laura: Hier hilft eine Wertetabelle. 4.3 Gemeinsame Punkte von Funktionsgraphen M2 M1 r1 r2 d (in cm) 0 1 2 3 4 5 6 7 8 K ( in f ___ m2 ) 4,50 3,00 1 – K(d) ____ K(0) (in %) 0 ≈ 33 3 __ 2 = % 3 __ 4 = % 3 __ 8 = % Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B ch ne r V rla gs