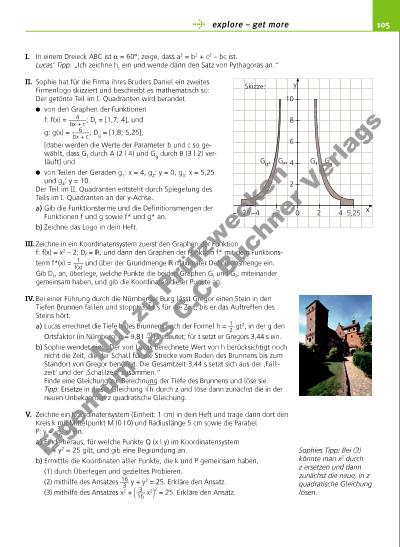
105 I. In einem Dreieck ABC ist α = 60°; zeige, dass a2 = b2 + c2 – bc ist. Lucas’ Tipp: „Ich zeichne hc ein und wende dann den Satz von Pythagoras an.“ II. Sophie hat für die Firma ihres Bruders Daniel ein zweites Firmenlogo skizziert und beschreibt es mathematisch so: Der getönte Teil im I. Quadranten wird berandet von den Graphen der Funktionen f: f(x) = 4 _____ bx + c ; Df = [1,7; 4], und g: g(x) = 6 _____ bx + c ; Dg = [1,8; 5,25], [dabei werden die Werte der Parameter b und c so gewählt, dass Gf durch A (2 | 4) und Gg durch B (3 | 2) verläuft] und von Teilen der Geraden g1: x = 4, g2: y = 0, g3: x = 5,25 und g4: y = 10. Der Teil im II. Quadranten entsteht durch Spiegelung des Teils im I. Quadranten an der y-Achse. a) Gib die Funktionsterme und die Defi nitionsmengen der Funktionen f und g sowie f* und g* an. b) Zeichne das Logo in dein Heft. III. Zeichne in ein Koordinatensystem zuerst den Graphen der Funktion f: f(x) = x2 – 2; Df = , und dann den Graphen der Funktion f* mit dem Funktions term f*(x) = 1 ___ f(x) und über der Grundmenge maximaler Defi nitionsmenge ein. Gib Df* an, überlege, welche Punkte die beiden Graphen Gf und Gf* miteinander gemeinsam haben, und gib die Koordinaten dieser Punkte an. IV. Bei einer Führung durch die Nürnberger Burg lässt Gregor einen Stein in den Tiefen Brunnen fallen und stoppt 3,44 s für die Zeit, bis er das Auftreffen des Steins hört. a) Lucas errechnet die Tiefe h des Brunnens nach der Formel h = 1 __ 2 gt2, in der g den Ortsfaktor (in Nürnberg: g ≈ 9,81 m __ s2 ) bedeutet; für t setzt er Gregors 3,44 s ein. b) Sophie wendet ein: „Der von Lucas berechnete Wert von h berücksichtigt noch nicht die Zeit, die der Schall für die Strecke vom Boden des Brunnens bis zum Standort von Gregor benötigt. Die Gesamtzeit 3,44 s setzt sich aus der ‚Fallzeit‘ und der ‚Schallzeit‘ zusammen.“ Finde eine Gleichung zur Berechnung der Tiefe des Brunnens und löse sie. Tipp: Ersetze in dieser Gleichung √ __ h durch z und löse dann zunächst die in der neuen Unbekannten z quadratische Gleichung. V. Zeichne ein Koordinatensystem (Einheit: 1 cm) in dein Heft und trage dann dort den Kreis k mit Mittelpunkt M (0 | 0) und Radiuslänge 5 cm sowie die Parabel P: y = 3 ___ 16 x2 ein. a) Finde heraus, für welche Punkte Q (x | y) im Koordinatensystem x2 + y2 = 25 gilt, und gib eine Begründung an. b) Ermittle die Koordinaten aller Punkte, die k und P gemeinsam haben, (1) durch Überlegen und gezieltes Probieren. (2) mithilfe des Ansatzes 16 ___ 3 y + y2 = 25. Erkläre den Ansatz. (3) mithilfe des Ansatzes x2 + ( 3 ___ 16 x2 ) 2 = 25. Erkläre den Ansatz. Sophies Tipp: Bei (3) könnte man x2 durch z ersetzen und dann zunächst die neue, in z quadratische Gleichung lösen. y x0 2 4 5,25–2 Skizze: –4–5,25 2 4 6 8 10 Gg* Gf* Gf Gg explore – get more Nu r z u Pr üf zw ec ke n Ei ge tu m de s C .C . B uc hn er V er la gs