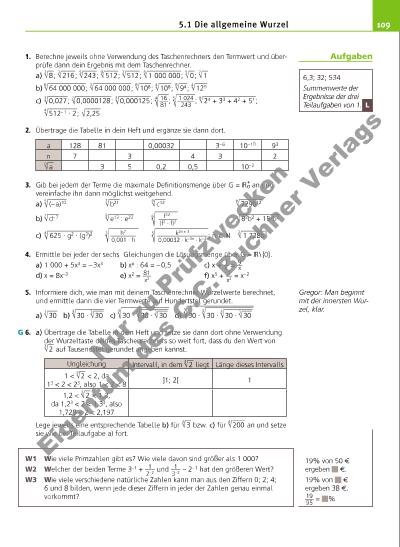
1095.1 Die allgemeine Wurzel 1. Berechne jeweils ohne Verwendung des Taschenrechners den Termwert und überprüfe dann dein Ergebnis mit dem Taschenrechner. a) 3 √ __ 8 ; 3 √ ____ 216 ; 5 √ ____ 243 ; 9 √ ____ 512 ; 3 √ ____ 512 ; 6 √ _________ 1 000 000 ; 5 √ __ 0 ; 7 √ __ 1 b) 6 √ __________ 64 000 000 ; 3 √ __________ 64 000 000 ; 8 √ ____ 108 ; 4 √ ____ 108 ; 8 √ ___ 94 ; 4 √ ____ 120 c) 3 √ ______ 0,027 ; 7 √ __________ 0,0000128 ; 3 √ _________ 0,000125 ; 4 √ ___ 16 ___ 81 ; 5 √ _____ 1 024_____ 243 ; 6 √ ______________ 24 + 33 + 42 + 51 ; 4 √ ________ 512– 1 · 2 ; √ ____ 2,25 2. Übertrage die Tabelle in dein Heft und ergänze sie dann dort. 3. Gib bei jedem der Terme die maximale Defi nitionsmenge über G = +0 an und vereinfache ihn dann möglichst weitgehend. a) 5 √ _____ (– a)10 7 √ ___ b21 4 √ ___ c12 6 √ ______ 729b12 b) 7 √ ___ d– 7 5 √ _______ e13 : e23 6 √ ______ f 12 ______ (f2 · f)2 √ ___________ 82b2 + 152b2 c) 4 √ ____________ 625 · g2 · (g3)2 3 √ ________ h 7 ________ 0,001 · h 5 √ ______________ k 2n + 3 _______________ 0,00032 · k–3n · k– 2 ; n X 3 √ _______ 1 728b6 4. Ermittle bei jeder der sechs Gleichungen die Lösungsmenge über G = \ {0}. a) 1 000 + 5x3 = – 3x3 b) x6 : 64 = – 0,5 c) x + 1 __ x = 9 __ x d) x = 8x–3 e) x2 = 81 ___ x2 f) x5 + 1 __ x2 = x– 2 5. Informiere dich, wie man mit deinem Taschenrechner Wurzelwerte berechnet, und ermittle dann die vier Termwerte auf Hundertstel gerundet. a) 3 √ ___ 30 b) 3 √ ________ 30 · 3 √ ___ 30 c) 3 √ _____________ 30 · 3 √ ________ 30 · 3 √ ___ 30 d) 3 √ __________________ 30 · 3 √ _____________ 30 · 3 √ ________ 30 · 3 √ ___ 30 6. a) Übertrage die Tabelle in dein Heft und setze sie dann dort ohne Verwendung der Wurzeltaste deines Taschenrechners so weit fort, dass du den Wert von 3 √ __ 2 auf Tausendstel gerundet angeben kannst. Lege jeweils eine entsprechende Tabelle b) für 3 √ __ 3 bzw. c) für 4 √ ____ 200 an und setze sie wie bei Teilaufgabe a) fort. W1 Wie viele Primzahlen gibt es? Wie viele davon sind größer als 1 000? W2 Welcher der beiden Terme 3–1 + 1 ___ 2– 2 und 1 ___ 3– 2 – 2– 1 hat den größeren Wert? W3 Wie viele verschiedene natürliche Zahlen kann man aus den Ziffern 0; 2; 4; 6 und 8 bilden, wenn jede dieser Ziffern in jeder der Zahlen genau einmal vorkommt? 6,3; 32; 534 Summenwerte der Ergebnisse der drei Teilaufgaben von 1. Gregor: Man beginnt mit der innersten Wurzel, klar. G a 128 81 0,00032 3– 6 10– 10 93 n 7 3 4 3 2 n √ __ a 3 5 0,2 0,5 10– 2 Ungleichung Intervall, in dem 3 √ __ 2 liegt Länge dieses Intervalls 1 < 3 √ __ 2 < 2, da 13 < 2 < 23, also 1 < 2 < 8 ]1; 2[ 1 1,2 < 3 √ __ 2 < 1,3, da 1,23 < 2 < 1,33, also 1,728 < 2 < 2,197 L Aufgaben 19% von 50 f ergeben f. 19% von f ergeben 38 f. 19 ___ 95 = % N r z u Pr üf zw ec ke n Ei g nt um d s C .C . B uc hn er V er la gs