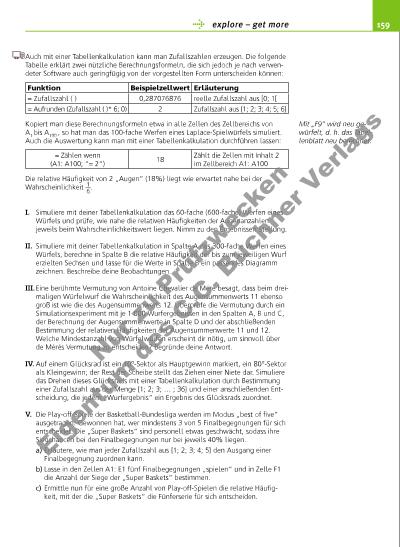
159 Auch mit einer Tabellenkalkulation kann man Zufallszahlen erzeugen. Die folgende Tabelle erklärt zwei nützliche Berechnungsformeln, die sich jedoch je nach verwendeter Software auch geringfügig von der vorgestellten Form unterscheiden können: Kopiert man diese Berechnungsformeln etwa in alle Zellen des Zellbereichs von A1 bis A100 , so hat man das 100-fache Werfen eines Laplace-Spielwürfels simuliert. Auch die Auswertung kann man mit einer Tabellenkalkulation durchführen lassen: Die relative Häufi gkeit von 2 „Augen“ (18%) liegt wie erwartet nahe bei der Wahrscheinlichkeit 1 __ 6 . I. Simuliere mit deiner Tabellenkalkulation das 60-fache (600-fache) Werfen eines Würfels und prüfe, wie nahe die relativen Häufi gkeiten der Augenanzahlen jeweils beim Wahrscheinlichkeitswert liegen. Nimm zu den Ergebnissen Stellung. II. Simuliere mit deiner Tabellenkalkulation in Spalte A das 300-fache Werfen eines Würfels, berechne in Spalte B die relative Häufi gkeit der bis zum jeweiligen Wurf erzielten Sechsen und lasse für die Werte in Spalte B ein passendes Diagramm zeichnen. Beschreibe deine Beobachtungen. III. Eine berühmte Vermutung von Antoine Chevalier de Méré besagt, dass beim dreimaligen Würfelwurf die Wahrscheinlichkeit des Augensummenwerts 11 ebenso groß ist wie die des Augensummenwerts 12. Überprüfe die Vermutung durch ein Simulationsexperiment mit je 1 000 Wurfergebnissen in den Spalten A, B und C, der Berechnung der Augensummenwerte in Spalte D und der abschließenden Bestimmung der relativen Häufi gkeiten der Augensummenwerte 11 und 12. Welche Mindestanzahl von Würfelwürfen erscheint dir nötig, um sinnvoll über de Mérés Vermutung zu entscheiden? Begründe deine Antwort. IV. Auf einem Glücksrad ist ein 10°-Sektor als Hauptgewinn markiert, ein 80°-Sektor als Kleingewinn; der Rest der Scheibe stellt das Ziehen einer Niete dar. Simuliere das Drehen dieses Glücksrads mit einer Tabellenkalkulation durch Bestimmung einer Zufallszahl aus der Menge {1; 2; 3; … ; 36} und einer anschließenden Entscheidung, die jedem „Wurfergebnis“ ein Ergebnis des Glücksrads zuordnet. V. Die Play-off-Spiele der Basketball-Bundesliga werden im Modus „best of fi ve“ ausgetragen: Gewonnen hat, wer mindestens 3 von 5 Finalbegegnungen für sich entscheidet. Die „Super Baskets“ sind personell etwas geschwächt, sodass ihre Siegchancen bei den Finalbegegnungen nur bei jeweils 40% liegen. a) Erläutere, wie man jeder Zufallszahl aus {1; 2; 3; 4; 5} den Ausgang einer Finalbegegnung zuordnen kann. b) Lasse in den Zellen A1: E1 fünf Finalbegegnungen „spielen“ und in Zelle F1 die Anzahl der Siege der „Super Baskets“ bestimmen. c) Ermittle nun für eine große Anzahl von Play-off-Spielen die relative Häufi gkeit, mit der die „Super Baskets“ die Fünferserie für sich entscheiden. Funktion Beispielzellwert Erläuterung = Zufallszahl ( ) 0,287076876 reelle Zufallszahl aus [0; 1[ = Aufrunden (Zufallszahl ( )* 6; 0) 2 Zufallszahl aus {1; 2; 3; 4; 5; 6} = Zählen wenn (A1: A100; “= 2“) 18 Zählt die Zellen mit Inhalt 2 im Zellbereich A1: A100 Mit „F9“ wird neu gewürfelt, d. h. das Tabellenblatt neu berechnet. explore – get more Nu r z u Pr üf zw ck en Ei ge nt um d es C .C . B uc h er V er la gs