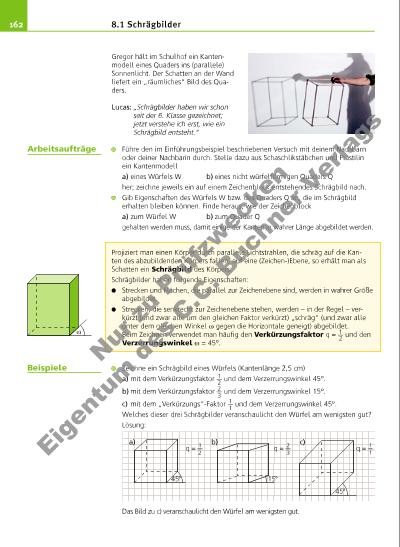
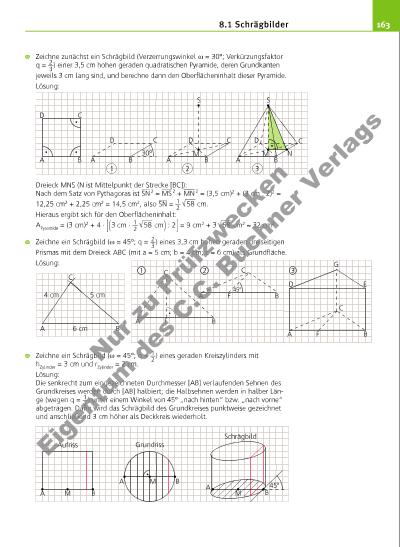
163 Zeichne zunächst ein Schrägbild (Verzerrungswinkel ω = 30°; Verkürzungsfaktor q = 2 __ 3 ) einer 3,5 cm hohen geraden quadratischen Pyramide, deren Grundkanten jeweils 3 cm lang sind, und berechne dann den Oberfl ächeninhalt dieser Pyramide. Lösung: Dreieck MNS (N ist Mittelpunkt der Strecke [BC]): Nach dem Satz von Pythagoras ist ___ SN 2 = ___ MS 2 + ____ MN 2 = (3,5 cm)2 + (3 cm : 2)2 = 12,25 cm2 + 2,25 cm2 = 14,5 cm2, also ___ SN = 1 __ 2 √ ___ 58 cm. Hieraus ergibt sich für den Oberfl ächeninhalt: APyramide = (3 cm) 2 + 4 · [ ( 3 cm · 1 __ 2 √ ___ 58 cm ) : 2 ] = 9 cm2 + 3 √ ___ 58 cm2 ≈ 32 cm2. Zeichne ein Schrägbild (ω = 45°; q = 2 __ 3 ) eines 3,3 cm hohen geraden dreiseitigen Prismas mit dem Dreieck ABC (mit a = 5 cm; b = 4 cm; c = 6 cm) als Grundfl äche. Lösung: Zeichne ein Schrägbild (ω = 45°; q = 1 __ 2 ) eines geraden Kreiszylinders mit hZylinder = 3 cm und rZylinder = 2 cm. Lösung: Die senkrecht zum eingezeichneten Durchmesser [AB] verlaufenden Sehnen des Grundkreises werden durch [AB] halbiert; die Halbsehnen werden in halber Länge (wegen q = 1 __ 2 ) unter einem Winkel von 45° „nach hinten“ bzw. „nach vorne“ abgetragen. Dann wird das Schrägbild des Grundkreises punktweise gezeichnet und anschließend 3 cm höher als Deckkreis wiederholt. A B D C A B D C 30° B D C A M S BA N 1 2 3 D C M S A B C 6 cm 5 cm4 cm A M B Aufriss A B Grundriss Schrägbild M BM A 45° A B C F A B C F 45° 1 2 A B C F 3 D E G 8.1 Schrägbilder Nu r z u Pr üf zw ec ke n Ei ge n m d es C .C . B uc hn er V er la gs