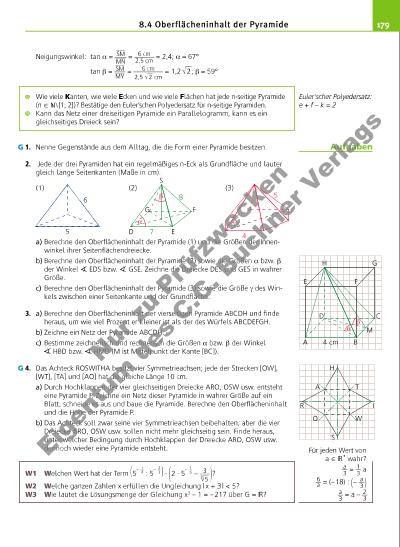
1798.4 Oberflächeninhalt der Pyramide Neigungswinkel: tan α = ___ SM ____ ____ MN = 6 cm ______ 2,5 cm = 2,4; α ≈ 67° tan β = ___ SM ____ ___ MY = 6 cm _________ 2,5 √ __ 2 cm = 1,2 √ __ 2 ; β ≈ 59° Wie viele Kanten, wie viele Ecken und wie viele Flächen hat jede n-seitige Pyramide (n X \ {1; 2})? Bestätige den Euler’schen Polyedersatz für n-seitige Pyramiden. Kann das Netz einer dreiseitigen Pyramide ein Parallelogramm, kann es ein gleichseitiges Dreieck sein? 1. Nenne Gegenstände aus dem Alltag, die die Form einer Pyramide besitzen. 2. Jede der drei Pyramiden hat ein regelmäßiges n-Eck als Grundfl äche und lauter gleich lange Seitenkanten (Maße in cm). a) Berechne den Oberfl ächeninhalt der Pyramide (1) und die Größen der Innenwinkel ihrer Seitenfl ächendreiecke. b) Berechne den Oberfl ächeninhalt der Pyramide (2) sowie die Größen α bzw. β der Winkel EDS bzw. GSE. Zeichne die Dreiecke DES und GES in wahrer Größe. c) Berechne den Oberfl ächeninhalt der Pyramide (3) sowie die Größe γ des Winkels zwischen einer Seitenkante und der Grundfl äche. 3. a) Berechne den Oberfl ächeninhalt der vierseitigen Pyramide ABCDH und fi nde heraus, um wie viel Prozent er kleiner ist als der des Würfels ABCDEFGH. b) Zeichne ein Netz der Pyramide ABCDH. c) Bestimme zeichnerisch und rechnerisch die Größen α bzw. β der Winkel HBD bzw. HMD (M ist Mittelpunkt der Kante [BC]). 4. Das Achteck ROSWITHA besitzt vier Symmetrieachsen; jede der Strecken [OW], [WT], [TA] und [AO] hat die gleiche Länge 10 cm. a) Durch Hochklappen der vier gleichseitigen Dreiecke ARO, OSW usw. entsteht eine Pyramide P. Zeichne ein Netz dieser Pyramide in wahrer Größe auf ein Blatt, schneide es aus und baue die Pyramide. Berechne den Oberfl ächeninhalt und die Höhe der Pyramide P. b) Das Achteck soll zwar seine vier Symmetrieachsen beibehalten, aber die vier Dreiecke ARO, OSW usw. sollen nicht mehr gleichseitig sein. Finde heraus, unter welcher Bedingung durch Hochklappen der Dreiecke ARO, OSW usw. dennoch wieder eine Pyramide entsteht. W1 Welchen Wert hat der Term ( 5 – 1 __ 4 : 5 – 2 __ 3 ) · ( 2 · 5 – 1 __ 6 – 3 ___ 6 √ __ 5 ) ? W2 Welche ganzen Zahlen x erfüllen die Ungleichung | x + 3 | < 5? W3 Wie lautet die Lösungsmenge der Gleichung x3 – 1 = – 217 über G = ? G (1) 6 5 (2) D E G F 8 7 α β (3) 5 4 γ S A B D C Mα β H G E F 4 cm A T O W H S R I G Euler‘scher Polyedersatz: e + f – k = 2 Für jeden Wert von a X + wahr? a __ 3 = 1 __ 3 a 6 __ a = (– 18) : ( – a __ 3 ) a __ 3 = a – 2 __ 3 Aufgaben N r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs