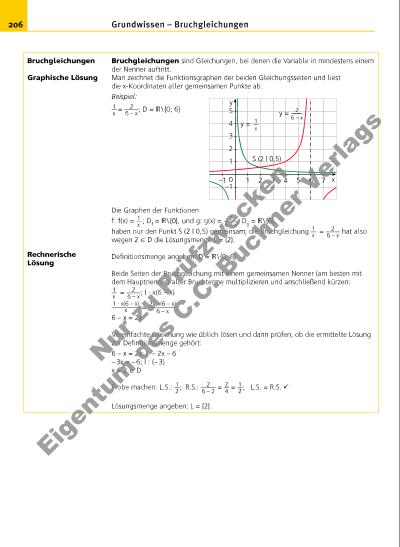
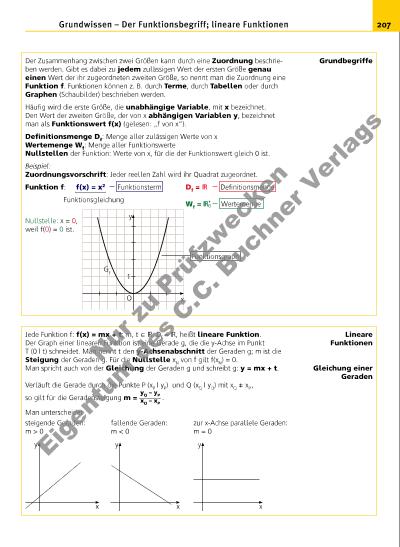
207Grundwissen – Der Funktionsbegriff; lineare Funktionen Der Zusammenhang zwischen zwei Größen kann durch eine Zuordnung beschrieben werden. Gibt es dabei zu jedem zulässigen Wert der ersten Größe genau einen Wert der ihr zugeordneten zweiten Größe, so nennt man die Zuordnung eine Funktion f. Funktionen können z. B. durch Terme, durch Tabellen oder durch Graphen (Schaubilder) beschrieben werden. Häufi g wird die erste Größe, die unabhängige Variable, mit x bezeichnet. Den Wert der zweiten Größe, der von x abhängigen Variablen y, bezeichnet man als Funktionswert f(x) (gelesen: „f von x“). Defi nitionsmenge Df: Menge aller zulässigen Werte von x Wertemenge Wf: Menge aller Funktionswerte Nullstellen der Funktion: Werte von x, für die der Funktionswert gleich 0 ist. Beispiel: Zuordnungsvorschrift: Jeder reellen Zahl wird ihr Quadrat zugeordnet. Funktion f: f(x) = x2 Df = Wf = 0 Nullstelle: x = 0, weil f(0) = 0 ist. Jede Funktion f: f(x) = mx + t; m, t X ; Df = , heißt lineare Funktion. Der Graph einer linearen Funktion ist eine Gerade g, die die y-Achse im Punkt T (0 | t) schneidet. Man nennt t den y-Achsenabschnitt der Geraden g; m ist die Steigung der Geraden g. Für die Nullstelle xN von f gilt f(xN) = 0. Man spricht auch von der Gleichung der Geraden g und schreibt g: y = mx + t. Verläuft die Gerade durch die Punkte P (xP | yP) und Q (xQ | yQ) mit xQ xP , so gilt für die Geradensteigung m = yQ – yP ______xQ – xP . Man unterscheidet steigende Geraden: fallende Geraden: zur x-Achse parallele Geraden: m > 0 m < 0 m = 0 Grundbegriffe Lineare Funktionen Gleichung einer Geraden x y x y x y x y 1 1 G f O Funktionsgleichung Funktionsterm Defi nitionsmenge Funktionsgraph Wertemenge Nu r z u Pr üf zw ec ke n Ei g nt m d es C .C . B uc hn er V er la gs