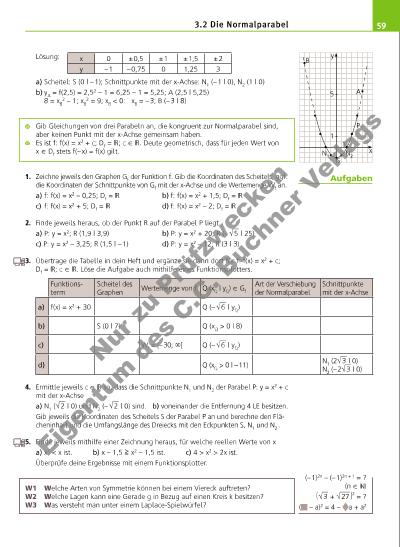
593.2 Die Normalparabel Lösung: a) Scheitel: S (0 | – 1); Schnittpunkte mit der x-Achse: N1 (– 1 | 0), N2 (1 | 0) b) yA = f(2,5) = 2,5 2 – 1 = 6,25 – 1 = 5,25; A (2,5 | 5,25) 8 = xB 2 – 1; xB 2 = 9; xB < 0: xB = – 3; B (– 3 | 8) Gib Gleichungen von drei Parabeln an, die kongruent zur Normalparabel sind, aber keinen Punkt mit der x-Achse gemeinsam haben. Es ist f: f(x) = x2 + c; Df = ; c X . Deute geometrisch, dass für jeden Wert von x X Df stets f(– x) = f(x) gilt. 1. Zeichne jeweils den Graphen Gf der Funktion f. Gib die Koordinaten des Scheitels, ggf. die Koordinaten der Schnittpunkte von Gf mit der x-Achse und die Wertemenge Wf an. a) f: f(x) = x2 – 0,25; Df = b) f: f(x) = x 2 + 1,5; Df = c) f: f(x) = x2 + 5; Df = d) f: f(x) = x 2 – 2; Df = 2. Finde jeweils heraus, ob der Punkt R auf der Parabel P liegt. a) P: y = x2; R (1,9 | 3,9) b) P: y = x2 + 20; R (– √ __ 5 | 25) c) P: y = x2 – 3,25; R (1,5 | – 1) d) P: y = x2 – 12; R (3 | 3) 3. Übertrage die Tabelle in dein Heft und ergänze sie dann dort für f: f(x) = x2 + c; Df = ; c X . Löse die Aufgabe auch mithilfe eines Funktionsplotters. 4. Ermittle jeweils c X so, dass die Schnittpunkte N1 und N2 der Parabel P: y = x 2 + c mit der x-Achse a) N1 ( √ __ 2 | 0) und N2 (– √ __ 2 | 0) sind. b) voneinander die Entfernung 4 LE besitzen. Gib jeweils die Koordinaten des Scheitels S der Parabel P an und berechne den Flächeninhalt und die Umfangslänge des Dreiecks mit den Eckpunkten S, N1 und N2 . 5. Finde jeweils mithilfe einer Zeichnung heraus, für welche reellen Werte von x a) x2 < x ist. b) x – 1,5 x2 – 1,5 ist. c) 4 > x2 > 2x ist. Überprüfe deine Ergebnisse mit einem Funktionsplotter. W1 Welche Arten von Symmetrie können bei einem Viereck auftreten? W2 Welche Lagen kann eine Gerade g in Bezug auf einen Kreis k besitzen? W3 Was versteht man unter einem Laplace-Spielwürfel? x 0 ± 0,5 ± 1 ± 1,5 ± 2 y – 1 – 0,75 0 1,25 3 Funktionsterm Scheitel des Graphen Wertemenge von f Q (xQ | yQ) X Gf Art der Verschiebung der Normalparabel Schnittpunkte mit der x-Achse a) f(x) = x2 + 30 Q (– √ __ 6 | yQ) b) S (0 | 7) Q (xQ > 0 | 8) c) Wf = [– 30; ∞[ Q (– √ __ 6 | yQ) d) Q (xQ > 0 | – 11) N1 (2 √ __ 3 | 0) N2 (– 2 √ __ 3 | 0) B 5 y xN2 A P S N1 1 1 Aufgaben (– 1)2n – (– 1)2n + 1 = ? (n X ) ( √ __ 3 + √ ___ 27 ) 2 = ? ( – a)2 = 4 – a + a2 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs