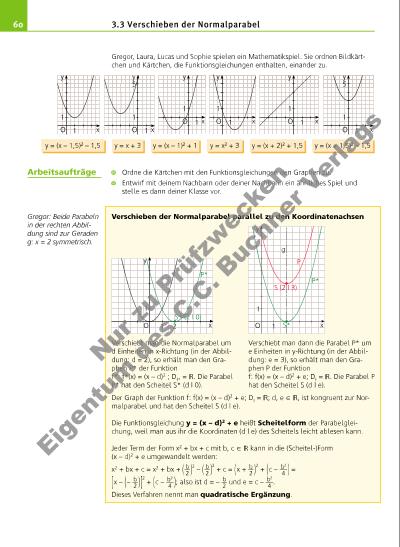
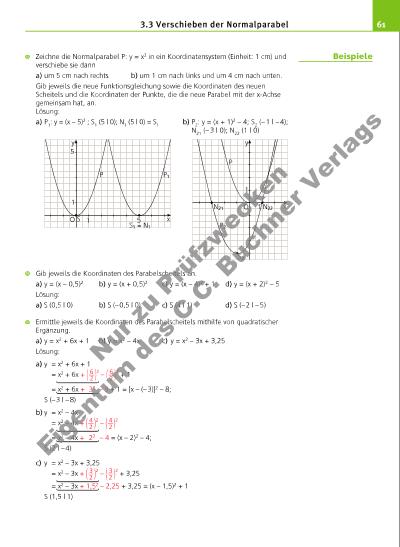
613.3 Verschieben der Normalparabel Zeichne die Normalparabel P: y = x2 in ein Koordinatensystem (Einheit: 1 cm) und verschiebe sie dann a) um 5 cm nach rechts b) um 1 cm nach links und um 4 cm nach unten. Gib jeweils die neue Funktionsgleichung sowie die Koordinaten des neuen Scheitels und die Koordinaten der Punkte, die die neue Parabel mit der x-Achse gemeinsam hat, an. Lösung: a) P1: y = (x – 5) 2 ; S1 (5 | 0); N1 (5 | 0) = S1 b) P2: y = (x + 1) 2 – 4; S2 (– 1 | – 4); N21 (– 3 | 0); N22 (1 | 0) Gib jeweils die Koordinaten des Parabelscheitels an. a) y = (x – 0,5)2 b) y = (x + 0,5)2 c) y = (x – 4)2 + 1 d) y = (x + 2)2 – 5 Lösung: a) S (0,5 | 0) b) S (– 0,5 | 0) c) S (4 | 1) d) S (– 2 | – 5) Ermittle jeweils die Koordinaten des Parabelscheitels mithilfe von quadratischer Ergänzung. a) y = x2 + 6x + 1 b) y = x2 – 4x c) y = x2 – 3x + 3,25 Lösung: a) y = x2 + 6x + 1 = x2 + 6x + ( 6 __ 2 ) 2 – ( 6 __ 2 ) 2 + 1 = x2 + 6x + 32 – 9 + 1 = [x – (– 3)]2 – 8; S (– 3 | – 8) b) y = x2 – 4x = x2 – 4x + ( 4 __ 2 ) 2 – ( 4 __ 2 ) 2 = x2 – 4x + 22 – 4 = (x – 2)2 – 4; S (2 | – 4) c) y = x2 – 3x + 3,25 = x2 – 3x + ( 3 __ 2 ) 2 – ( 3 __ 2 ) 2 + 3,25 = x2 – 3x + 1,52 – 2,25 + 3,25 = (x – 1,5)2 + 1 S (1,5 | 1) xO 1 y 1 5S P P1 S1 = N1 5 xO 1 y 1 P P2 N21 S2 N22 Beispiele Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs