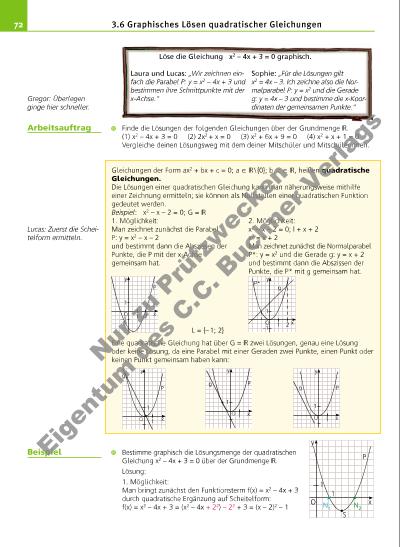
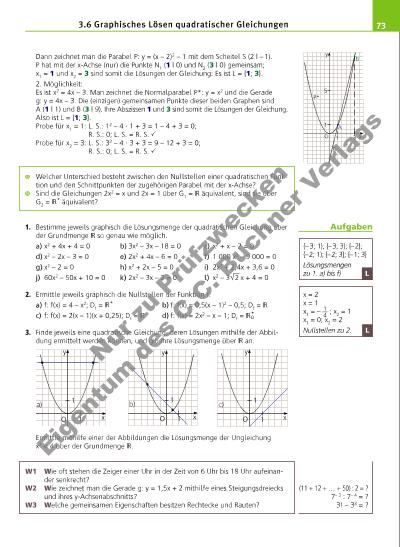
73 Dann zeichnet man die Parabel P: y = (x – 2)2 – 1 mit dem Scheitel S (2 | – 1). P hat mit der x-Achse (nur) die Punkte N1 (1 | 0) und N2 (3 | 0) gemeinsam; x1 = 1 und x2 = 3 sind somit die Lösungen der Gleichung: Es ist L = {1; 3}. 2. Möglichkeit: Es ist x2 = 4x – 3. Man zeichnet die Normalparabel P*: y = x2 und die Gerade g: y = 4x – 3. Die (einzigen) gemeinsamen Punkte dieser beiden Graphen sind A (1 | 1) und B (3 | 9). Ihre Abszissen 1 und 3 sind somit die Lösungen der Gleichung. Also ist L = {1; 3}. Probe für x1 = 1: L. S.: 1 2 – 4 · 1 + 3 = 1 – 4 + 3 = 0; R. S.: 0; L. S. = R. S. Probe für x2 = 3: L. S.: 3 2 – 4 · 3 + 3 = 9 – 12 + 3 = 0; R. S.: 0; L. S. = R. S. Welcher Unterschied besteht zwischen den Nullstellen einer quadratischen Funktion und den Schnittpunkten der zugehörigen Parabel mit der x-Achse? Sind die Gleichungen 2x2 = x und 2x = 1 über G1 = äquivalent, sind sie über G2 = + äquivalent? 1. Bestimme jeweils graphisch die Lösungsmenge der quadratischen Gleichung über der Grundmenge so genau wie möglich. a) x2 + 4x + 4 = 0 b) 3x2 – 3x – 18 = 0 c) x2 + x – 2 = 0 d) x2 – 2x – 3 = 0 e) 2x2 + 4x – 6 = 0 f) 1 000 x2 – 9 000 = 0 g) x2 – 2 = 0 h) x2 + 2x – 5 = 0 i) 2x2 + 2,4x + 3,6 = 0 j) 60x2 – 50x + 10 = 0 k) 2x2 – 3x – 2 = 0 l) x2 – 3 √ __ 2 x + 4 = 0 2. Ermittle jeweils graphisch die Nullstellen der Funktion f. a) f: f(x) = 4 – x2; Df = + b) f: f(x) = 0,5(x – 1)2 – 0,5; Df = c) f: f(x) = 2(x – 1)(x + 0,25); Df = d) f: f(x) = 2x 2 – x – 1; Df = + 0 3. Finde jeweils eine quadratische Gleichung, deren Lösungen mithilfe der Abbildung ermittelt werden können, und gib ihre Lösungsmenge über an. Ermittle mithilfe einer der Abbildungen die Lösungsmenge der Ungleichung x2 < 4 über der Grundmenge . W1 Wie oft stehen die Zeiger einer Uhr in der Zeit von 6 Uhr bis 18 Uhr aufeinander senkrecht? W2 Wie zeichnet man die Gerade g: y = 1,5x + 2 mithilfe eines Steigungsdreiecks und ihres y-Achsenabschnitts? W3 Welche gemeinsamen Eigenschaften besitzen Rechtecke und Rauten? 3.6 Graphisches Lösen quadratischer Gleichungen {– 3; 1}; {– 3; 3}; {– 2}; {– 2; 1); {– 2; 3}; {– 1; 3} Lösungsmengen zu 1. a) bis f) x = 2 x = 1 x1 = – 1 __ 4 ; x2 = 1 x1 = 0; x2 = 2 Nullstellen zu 2. 1 1 y xO a) 1 1 y xO b) 1 1 y xO c) 1 1 y x P* A g 3 5 B O L L Aufgaben (11 + 12 + … + 50) : 2 = ? 7– 3 : 7– 4 = ? 3! – 33 = ? Nu r z u Pr üf zw ck en Ei ge nt um d es C .C . B uc hn er V er la gs