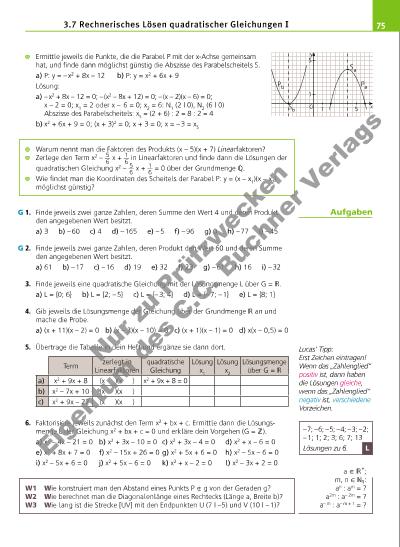
75 Ermittle jeweils die Punkte, die die Parabel P mit der x-Achse gemeinsam hat, und fi nde dann möglichst günstig die Abszisse des Parabelscheitels S. a) P: y = – x2 + 8x – 12 b) P: y = x2 + 6x + 9 Lösung: a) – x2 + 8x – 12 = 0; – (x2 – 8x + 12) = 0; – (x – 2)(x – 6) = 0; x – 2 = 0; x1 = 2 oder x – 6 = 0; x2 = 6: N1 (2 | 0), N2 (6 | 0) Abszisse des Parabelscheitels: xS = (2 + 6) : 2 = 8 : 2 = 4 b) x2 + 6x + 9 = 0; (x + 3)2 = 0; x + 3 = 0; x = – 3 = xS Warum nennt man die Faktoren des Produkts (x – 5)(x + 7) Linearfaktoren? Zerlege den Term x2 – 5 __ 6 x + 1 __ 6 in Linearfaktoren und fi nde dann die Lösungen der quadratischen Gleichung x2 – 5 __ 6 x + 1 __ 6 = 0 über der Grundmenge . Wie fi ndet man die Koordinaten des Scheitels der Parabel P: y = (x – x1)(x – x2) möglichst günstig? 1. Finde jeweils zwei ganze Zahlen, deren Summe den Wert 4 und deren Produkt den angegebenen Wert besitzt. a) 3 b) – 60 c) 4 d) – 165 e) – 5 f) – 96 g) 0 h) – 77 i) – 45 2. Finde jeweils zwei ganze Zahlen, deren Produkt den Wert 60 und deren Summe den angegebenen Wert besitzt. a) 61 b) – 17 c) – 16 d) 19 e) 32 f) 23 g) – 61 h) 16 i) – 32 3. Finde jeweils eine quadratische Gleichung mit der Lösungsmenge L über G = . a) L = {0; 6} b) L = {2; – 5} c) L = {– 3; 4} d) L = {– 7; – 1} e) L = {8; 1} 4. Gib jeweils die Lösungsmenge der Gleichung über der Grundmenge an und mache die Probe. a) (x + 11)(x – 2) = 0 b) (x – 3)(x – 10) = 0 c) (x + 1)(x – 1) = 0 d) x(x – 0,5) = 0 5. Übertrage die Tabelle in dein Heft und ergänze sie dann dort. 6. Faktorisiere jeweils zunächst den Term x2 + bx + c. Ermittle dann die Lösungsmenge L der Gleichung x2 + bx + c = 0 und erkläre dein Vorgehen (G = ). a) x2 – 4x – 21 = 0 b) x2 + 3x – 10 = 0 c) x2 + 3x – 4 = 0 d) x2 + x – 6 = 0 e) x2 + 8x + 7 = 0 f) x2 – 15x + 26 = 0 g) x2 + 5x + 6 = 0 h) x2 – 5x – 6 = 0 i) x2 – 5x + 6 = 0 j) x2 + 5x – 6 = 0 k) x2 + x – 2 = 0 l) x2 – 3x + 2 = 0 W1 Wie konstruiert man den Abstand eines Punkts P x g von der Geraden g? W2 Wie berechnet man die Diagonalenlänge eines Rechtecks (Länge a, Breite b)? W3 Wie lang ist die Strecke [UV] mit den Endpunkten U (7 | –5) und V (10 | – 1)? 3.7 Rechnerisches Lösen quadratischer Gleichungen I – 7; – 6; – 5; – 4; – 3; – 2; – 1; 1; 2; 3; 6; 7; 13 Lösungen zu 6. Lucas’ Tipp: Erst Zeichen eintragen! Wenn das „Zahlenglied“ positiv ist, dann haben die Lösungen gleiche, wenn das „Zahlenglied“ negativ ist, verschiedene Vorzeichen. G G Term zerlegt in Linearfaktoren quadratische Gleichung Lösung x1 Lösung x2 Lösungsmenge über G = a) x2 + 9x + 8 (x )(x ) x2 + 9x + 8 = 0 b) x2 – 7x + 10 (x )(x ) c) x2 + 9x – 22 (x )(x ) 1 1 y xOSb 5 Sa Pb Pa 5 L Aufgaben a X + ; m, n X : an : am = ? a2m : a– 2m = ? a– m : a– m + 1 = ? Nu r z u Pr üf zw ec ke n Ei g nt um d s C .C . B uc hn er V er la gs