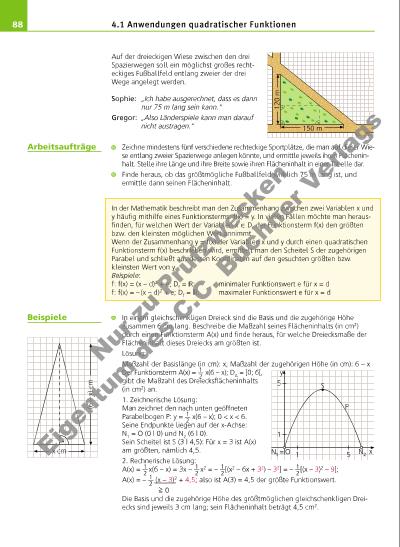
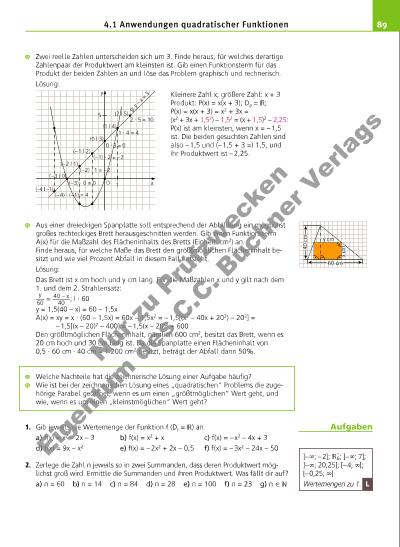
89 1O 5 y x (–4 | –1) (–3 | 0) (–2 | 1) (–1 | 2) (0 | 3) (1 | 4) (2 | 5) g: y – x = 3 2 · 5 = 10 1 · 4 = 4 0 · 3 = 0 (–1) · 2 = –2 (–2) · 1 = –2 (–3) · 0 = 0 (–4) · (–1) = 4 Zwei reelle Zahlen unterscheiden sich um 3. Finde heraus, für welches derartige Zahlenpaar der Produktwert am kleinsten ist. Gib einen Funktionsterm für das Produkt der beiden Zahlen an und löse das Problem graphisch und rechnerisch. Lösung: Kleinere Zahl x; größere Zahl: x + 3 Produkt: P(x) = x(x + 3); DP = ; P(x) = x(x + 3) = x2 + 3x = (x2 + 3x + 1,52) – 1,52 = (x + 1,5)2 – 2,25: P(x) ist am kleinsten, wenn x = – 1,5 ist. Die beiden gesuchten Zahlen sind also – 1,5 und (– 1,5 + 3 =) 1,5, und ihr Produktwert ist – 2,25. Aus einer dreieckigen Spanplatte soll entsprechend der Abbildung ein möglichst großes rechteckiges Brett herausgeschnitten werden. Gib einen Funktionsterm A(x) für die Maßzahl des Flächeninhalts des Bretts (Einheit: cm2) an. Finde heraus, für welche Maße das Brett den größtmöglichen Flächeninhalt besitzt und wie viel Prozent Abfall in diesem Fall entsteht. Lösung: Das Brett ist x cm hoch und y cm lang. Für die Maßzahlen x und y gilt nach dem 1. und dem 2. Strahlensatz: y ___ 60 = 40 – x _____ 40 ; | · 60 y = 1,5(40 – x) = 60 – 1,5x A(x) = xy = x · (60 – 1,5x) = 60x – 1,5x2 = – 1,5[(x2 – 40x + 202) – 202] = – 1,5[(x – 20)2 – 400] = – 1,5(x – 20)2 + 600 Den größtmöglichen Flächeninhalt, nämlich 600 cm2, besitzt das Brett, wenn es 20 cm hoch und 30 cm lang ist. Da die Spanplatte einen Flächeninhalt von 0,5 · 60 cm · 40 cm = 1 200 cm2 besitzt, beträgt der Abfall dann 50%. Welche Nachteile hat die zeichnerische Lösung einer Aufgabe häufi g? Wie ist bei der zeichnerischen Lösung eines „quadratischen“ Problems die zugehörige Parabel geöffnet, wenn es um einen „größtmöglichen“ Wert geht, und wie, wenn es um einen „kleinstmöglichen“ Wert geht? 1. Gib jeweils die Wertemenge der Funktion f (Df = ) an. a) f(x) = x2 – 2x – 3 b) f(x) = x2 + x c) f(x) = – x2 – 4x + 3 d) f(x) = 9x – x2 e) f(x) = – 2x2 + 2x – 0,5 f) f(x) = – 3x2 – 24x – 50 2. Zerlege die Zahl n jeweils so in zwei Summanden, dass deren Produktwert möglichst groß wird. Ermittle die Summanden und ihren Produktwert. Was fällt dir auf? a) n = 60 b) n = 14 c) n = 84 d) n = 28 e) n = 100 f) n = 23 g) n X 4.1 Anwendungen quadratischer Funktionen ]– ∞; – 2]; 0; ]– ∞; 7]; ]– ∞; 20,25]; [– 4; ∞[; [– 0,25; ∞[ Wertemengen zu 1. 60 cm y cm x cm 40 c m L Aufgaben Nu r z u Pr üf zw ec ke n Ei g nt um d es C. C. Bu ch ne r V er la gs