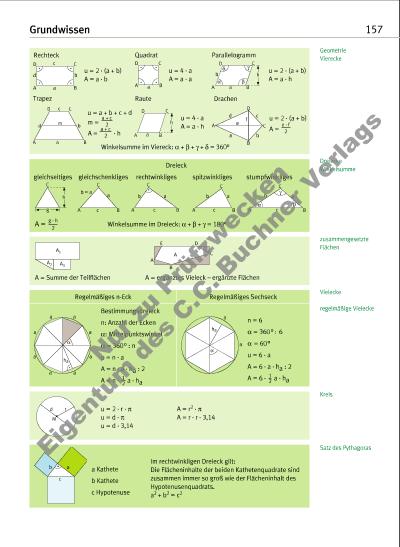
Grundwissen 157 Geometrie Vierecke Rechteck u = 2 · (a + b) A = a · b D A C Ba b c d D A C Ba D A C Ba b h a b gd D A C B h a Dreiecke Winkelsumme Dreieck gleichseitiges gleichschenkliges rechtwinkliges spitzwinkliges stumpfwinkliges A = Winkelsumme im Dreieck: a + b + g = 180° g · h 2 A h g C A C Bc a b = a b A C B a c A C B b a c A C B b a c ba g Vielecke regelmäßige Vielecke Regelmäßiges n-Eck Bestimmungsdreieck n: Anzahl der Ecken a: Mittelpunktswinkel a = 360° : n u = n · a A = n · a · ha : 2 A = n · a · ha 1 2 Regelmäßiges Sechseck a a a a aa a a ha a n = 6 a = 360°: 6 a = 60° u = 6 · a A = 6 · a · ha : 2 A = 6 · a · ha 1 2 a a ha a Kreis u = 2 · r · p u = d · p u = d · 3,14 A = r2 · p A = r · r · 3,14M d r zusammengesetzte Flächen A B C DE A A1 A2 A3 A = Summe der Teilflächen A = ergänztes Vieleck – ergänzte Flächen Satz des Pythagoras ab c a Kathete b Kathete c Hypotenuse Im rechtwinkligen Dreieck gilt: Die Flächeninhalte der beiden Kathetenquadrate sind zusammen immer so groß wie der Flächen inhalt des Hypotenusenquadrats. a2 + b2 = c2 Drachen u = 2 · (a + b) A = e · f 2 Parallelogramm u = 2 · (a + b) A = a · h Quadrat u = 4 · a A = a · a D A C B a d b c e f Trapez u = a + b + c + d m = a + c 2 D A C B m a c d b Raute u = 4 · a A = a · h A = · h a + c 2 Winkelsumme im Viereck: a + b + g + d = 360° Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs