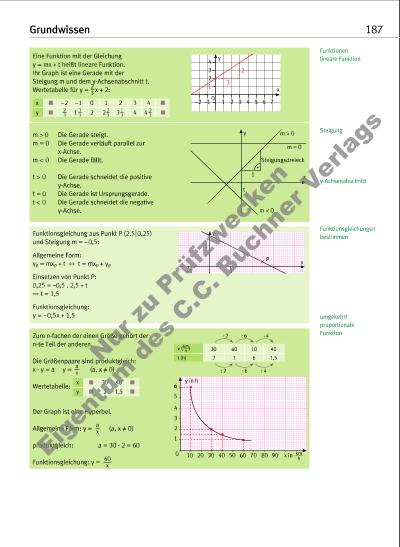
Grundwissen 187 Funktionsgleichungen bestimmen Funktionsgleichung aus Punkt P (2,5 B0,25) und Steigung m = –0,5: Allgemeine Form: yP = mxP + t c t = mxP + yP Einsetzen von Punkt P: 0,25 = –0,5 . 2,5 + t b t = 1,5 Funktionsgleichung: y = –0,5x + 1,5 Funktionen lineare Funktion Steigung y-Achsenabschnitt Eine Funktion mit der Gleichung y = mx + t heißt lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung m und dem y-Achsenabschnitt t. Wertetabelle für y = x + 2: m > 0 Die Gerade steigt. m = 0 Die Gerade verläuft parallel zur x-Achse. m < 0 Die Gerade fällt. t > 0 Die Gerade schneidet die positive y-Achse. t = 0 Die Gerade ist Ursprungsgerade. t < 0 Die Gerade schneidet die negative y-Achse. x M –2 –1 0 1 2 3 4 M y M 1 2 2 3 4 4 M y 4 3 2 1 0 1 2 3 4 5 x 6 7–1–2 2 3 y 1 x m = 0 t Steigungsdreieck m < 0 m > 0 2 3 1 3 2 3 1 3 2 3 2 3 umgekehrt proportionale Funktion v ( ) 30 60 10 40 t (h) 2 1 6 1,5 km h · 2 : 6 4 : 2 6 : 4 0 10 20 30 40 80 1 2 3 4 5 6 y in h 50 60 70 km h 90 x in · · Zum n-fachen der einen Größe gehört der n-te Teil der anderen. Die Größenpaare sind produktgleich: x · y = a y = (a, x " 0) Wertetabelle: Der Graph ist eine Hyperbel. Allgemeine Form: y = (a, x " 0) produktgleich: a = 30 · 2 = 60 Funktionsgleichung: y = a x a x 60 x x M 30 40 M y M 2 1,5 M 1 y P x 1 –1 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs