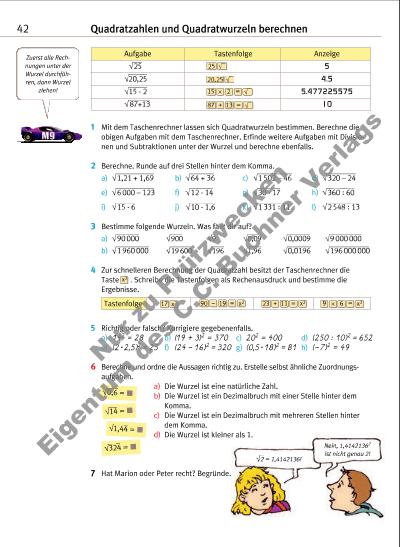
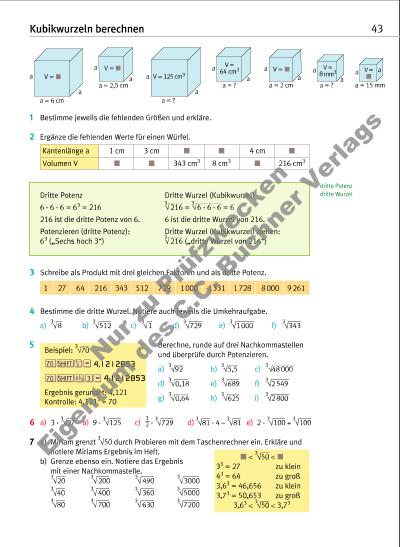
Kubikwurzeln berechnen 43 1 Bestimme jeweils die fehlenden Größen und erkläre. 2 Ergänze die fehlenden Werte für einen Würfel. 3 Schreibe als Produkt mit drei gleichen Faktoren und als dritte Potenz. 4 Bestimme die dritte Wurzel. Notiere auch jeweils die Umkehraufgabe. 6 a) 3 · 3 27 b) 9 · 3 125 c) · 3 729 d) 3 81 · 4 – 3 81 e) 2 · 3 100 + 3 100 7 a) Miriam grenzt 3 50 durch Probieren mit dem Taschenrechner ein. Erkläre und notiere Miriams Ergebnis im Heft. b) Grenze ebenso ein. Notiere das Ergebnis mit einer Nachkommastelle. 3 20 3 200 3 490 3 3000 V = Ma a a = 6 cm V = Ma a a = 2 cm V = Ma a a = 2,5 cm a = 15 mm aa V = MV = 125 cm3a a a = ? V = 64 cm3 a a a = ? V = 8 mm3 a a a = ? Beispiel: 3 70 4,1212853 4, 4,1212853 Ergebnis gerundet: 4,121 Kontrolle: 4,1213 ) 70 1 27 64 216 343 512 729 1000 1331 1 728 8 000 9 261 a) 3 8 b) 3 512 c) 3 1 d) 3 729 e) 3 1000 f) 3 343 5 Berechne, runde auf drei Nachkomma stellen und überprüfe durch Potenzieren. a) 3 92 b) 3 5,5 c) 3 48 000 d) 3 0,18 e) 3 689 f) 3 2 549 g) 3 0,64 h) 3 625 i) 3 2 800 1 2 =70 SHIFT 3 370 SHIFT x1 =y dritte Potenz dritte WurzelDritte Potenz 6 · 6 · 6 = 63 = 216 216 ist die dritte Potenz von 6. Potenzieren (dritte Potenz): 63 („Sechs hoch 3“) Dritte Wurzel (Kubikwurzel) 216 = 6 · 6 · 6 = 6 6 ist die dritte Wurzel von 216. Dritte Wurzel (Kubikwurzel) ziehen: 216 („dritte Wurzel von 216“) Kantenlänge a 1 cm 3 cm M M 4 cm M Volumen V M M 343 cm3 8 cm3 M 216 cm3 3 3 3 3 40 3 400 3 360 3 5000 3 80 3 700 3 630 3 7200 M < 3 50 < M 33 = 27 zu klein 43 = 64 zu groß 3,63 = 46,656 zu klein 3,73 = 50,653 zu groß 3,63 < 3 50 < 3,73 Nu r z u Pr üf zw ec ke n E ge nt um d es C .C . B uc hn er V er la gs