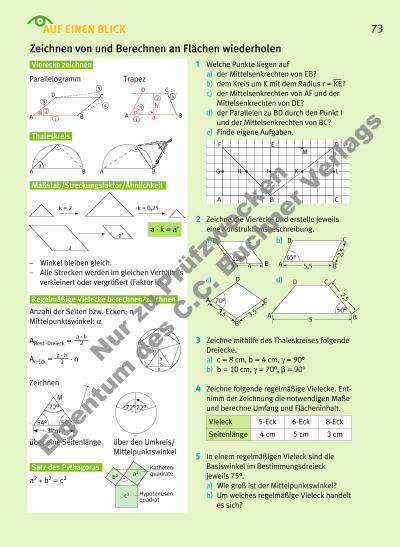
AUF EINEN BLICK Zeichnen von und Berechnen an Flächen wiederholen 1 Welche Punkte liegen auf a) der Mittelsenkrechten von EB? b) dem Kreis um K mit dem Radius r = KE? c) der Mittelsenkrechten von AF und der Mittelsenkrechten von DE? d) der Parallelen zu BD durch den Punkt I und der Mittelsenkrechten von BC? e) Finde eigene Aufgaben. 2 Zeichne die Vierecke und erstelle jeweils eine Konstruktionsbeschreibung. 3 Zeichne mithilfe des Thaleskreises folgende Dreiecke. a) c = 8 cm, b = 4 cm, g = 90° b) b = 10 cm, g = 70°, b = 90° 4 Zeichne folgende regelmäßige Vielecke. Entnimm der Zeichnung die notwendigen Maße und berechne Umfang und Flächeninhalt. 5 In einem regelmäßigen Vieleck sind die Basiswinkel im Bestimmungsdreieck jeweils 75°. a) Wie groß ist der Mittelpunktswinkel? b) Um welches regelmäßige Vieleck handelt es sich? Regelmäßige Vielecke berechnen/zeichnen Satz des Pythagoras 73 Parallelogramm Trapez r h a a 7272 °° M 3 cm 54° 54° 72° a2 b2 c2 Kathetenquadrate Hypotenusenquadrat Anzahl der Seiten bzw. Ecken: n Mittelpunktswinkel: a ABest.-Dreieck = a · h 2 über den Umkreis/ Mittelpunktswinkel über eine Seitenlänge Zeichnen a2 + b2 = c2 a) b) c) d) 5,5 65° A B D C 5 A 4 B D C 128° 2 ,5 5, 5 50° A B D C 2,5 70° 3,5 A B D C 3,5 4 A B C D M EF G H LI K CD a 1 3 4 5 2 A B a 1 2 A a B h3 4 D C a A B A B k = 2 k = 0,25 a a’ – Winkel bleiben gleich. – Alle Strecken werden im gleichen Verhältnis verkleinert oder vergrößert (Faktor k). a · k = a’ Vieleck 5-Eck 6-Eck 8-Eck Seitenlänge 4 cm 5 cm 3 cm Vierecke zeichnen Maßstab/Streckungsfaktor/Ähnlichkeit Thaleskreis An-Eck = · n a · h 2 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn r V er la gs