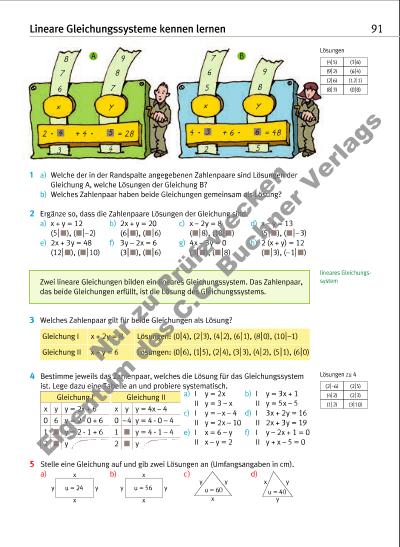
Lineare Gleichungssysteme kennen lernen 91 4 Bestimme jeweils das Zahlenpaar, welches die Lösung für das Gleichungssystem ist. Lege dazu eine Tabelle an und probiere systematisch. 5 Stelle eine Gleichung auf und gib zwei Lösungen an (Umfangsangaben in cm). a) b) c) d) a) I y = 2x b) I y = 3x + 1 II y = 3 – x II y = 5x – 5 c) I y = –x – 4 d) I 3x + 2y = 16 II y = 2x – 10 II 2x + 3y = 19 e) I x = 6 – y f) I y – 2x + 1 = 0 II x – y = 2 II y + x – 5 = 0 Gleichung I x y y = 2x + 6 0 6 y = 2 · 0 + 6 1 M y = 2 · 1 + 6 2 M y 1 a) Welche der in der Randspalte angegebenen Zahlenpaare sind Lösungen der Gleichung A, welche Lösungen der Gleichung B? b) Welches Zahlenpaar haben beide Gleichungen gemeinsam als Lösung? 2 Ergänze so, dass die Zahlenpaare Lösungen der Gleichung sind. a) x + y = 12 b) 2x + y = 20 c) x – 2y = 8 d) x – y = 13 (5 BM), (MB–2) (6 BM), (MB6) (MB8), (10 BM) (5 BM), (MB–3) e) 2x + 3y = 48 f) 3y – 2x = 6 g) 4x – 3y = 0 h) 2 (x + y) = 12 (12 BM), (MB10) (3 BM), (MB6) (3 BM), (MB8) (MB3), (–1BM) Gleichung I x + 2y = 8 Lösungen: (0 B4), (2 B3), (4 B2), (6 B1), (8 B0), (10 B–1) Gleichung II x + y = 6 Lösungen: (0 B6), (1B5), (2 B4), (3 B3), (4 B2), (5 B1), (6 B0) Gleichung II x y y = 4x – 4 0 –4 y = 4 · 0 – 4 1 M y = 4 · 1 – 4 2 M y x x y yu = 24 x x y yu = 56 x y y u = 60 y x y u = 40 3 Welches Zahlenpaar gilt für beide Gleichungen als Lösung? Zwei lineare Gleichungen bilden ein lineares Gleichungssystem. Das Zahlenpaar, das beide Gleichungen erfüllt, ist die Lösung des Gleichungssys tems. A B lineares Gleichungs system Lösungen (4 B5) (3 B6) (9 B2) (6 B4) (2 B6) (12 B1) (8 B3) (0 B8) Lösungen zu 4 (2 B–6) (2 B5) (4 B2) (2 B3) (1 B2) (3 B10) 8 7 6 3 9 8 7 4 x 2 • M + 4 • M = 28 y 7 6 5 2 9 8 5 x 4 • M + 6 • M = 48 y 3 64 5 Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs