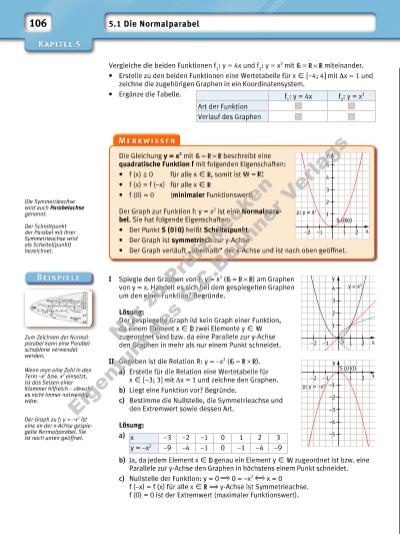
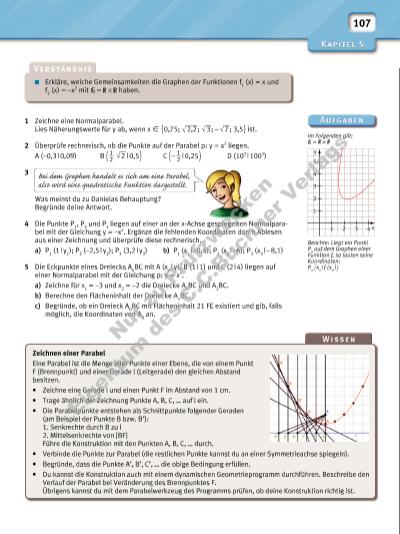
11 2 3 4 x 2 3 4 5 y Bei dem Graphen handelt es sich um eine Parabel, also wird eine quadratische Funktion dargestellt. 107 Zeichnen einer Parabel Eine Parabel ist die Menge aller Punkte einer Ebene, die von einem Punkt F (Brennpunkt) und einer Gerade l (Leit gerade) den gleichen Abstand besitzen. • Zeichne eine Gerade l und einen Punkt F im Abstand von 1 cm. • Trage ähnlich der Zeichnung Punkte A, B, C, … auf l ein. • Die Parabelpunkte entstehen als Schnittpunkte folgender Geraden (am Beispiel der Punkte B bzw. B’): 1. Senkrechte durch B zu l 2. Mittelsenkrechte von [BF] Führe die Konstruktion mit den Punkten A, B, C, … durch. • Verbinde die Punkte zur Parabel (die restlichen Punkte kannst du an einer Symmetrieachse spiegeln). • Begründe, dass die Punkte A’, B’, C’, … die obige Bedingung erfüllen. • Du kannst die Konstruktion auch mit einem dynamischen Geometrie programm durchführen. Beschreibe den Verlauf der Parabel bei Veränderung des Brennpunktes F. Übrigens kannst du mit dem Parabelwerkzeug des Programms prüfen, ob deine Konstruktion richtig ist. 1 Zeichne eine Normalparabel. Lies Näherungswerte für y ab, wenn x X { 0,75; √ ___ 2,2 ; √ __ 3 ; – √ __ 7 ; 3,5 } ist. 2 Überprüfe rechnerisch, ob die Punkte auf der Parabel p: y = x2 liegen. A (–0,3 | 0,09) B ( 1 __ 2 √ __ 2 | 0,5 ) C ( – 1 __ 2 | 0,25 ) D (103 | 1003) 3 Was meinst du zu Danielas Behauptung? Begründe deine Antwort. 4 Die Punkte P1, P2 und P3 liegen auf einer an der x-Achse gespiegelten Normalparabel mit der Gleichung y = –x2. Ergänze die fehlenden Koordinaten durch Ablesen aus einer Zeichnung und überprüfe diese rechnerisch. a) P1 (1 | y1); P2 (–2,5 | y2); P3 (3,2 | y3) b) P1 (x1 | –0,4); P2 (x2 | –6); P3 (x3 | – 8,1) 5 Die Eckpunkte eines Dreiecks AnBC mit A (xn | y), B (1 | 1) und C (2 | 4) liegen auf einer Normalparabel mit der Gleichung p: y = x2. a) Zeichne für x1 = –3 und x2 = –2 die Dreiecke A1BC und A2BC. b) Berechne den Flächen inhalt der Dreiecke AnBC. c) Begründe, ob ein Dreieck A0BC mit Flächeninhalt 21 FE existiert und gib, falls möglich, die Koordinaten von A0 an. Erkläre, welche Gemeinsamkeiten die Graphen der Funktionen f1 (x) = x und f2 (x) = –x 2 mit = haben. Im Folgenden gilt: = Beachte: Liegt ein Punkt Pn auf dem Graphen einer Funktion f, so lauten seine Koordinaten: Pn ( xn | f (xn ) ) Nu r z u Pr üf zw ck en Ei g nt um d es C .C .B uc hn er V er la gs