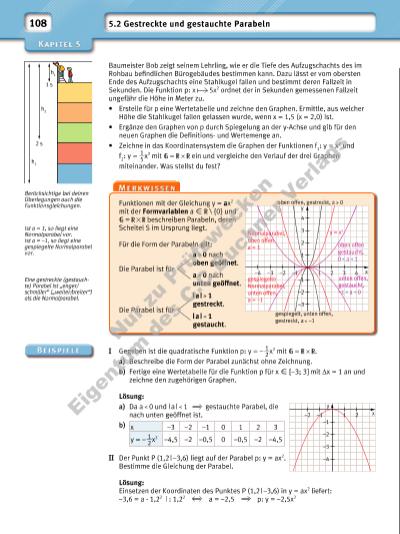
10 –1 –2 –1 1 2 x y –2 –3 2 p 1 p 2 p 4 p 5 p 3 3 4 5 109 Beschreibe den Verlauf des Graphen zu y = ax2 mit = , wenn die Formvariable a = 0 ist. Ändert sich die Funktionsgleichung p: y = ax2 mit a X \ {0} und = , wenn der zugehörige Graph an der y-Achse gespiegelt wird? Begründe. 1 Zeichne den Graphen der Funktion f im angegebenen Intervall. a) f: y = 1,2x2 x X [–3; 3] Δx = 1 b) f: y = –2x2 x X [–2; 2] Δx = 0,5 c) f: y= 0,75x2 x X [–3; 3] Δx = 1 d) f: y = – 1 __ 3 x 2 x X [–4; 4] Δx = 0,5 2 Ordne den Graphen in der Randspalte die entsprechende Funktionsgleichung zu. A y = 0,1x2 B y = – 2 __ 7 x 2 C y = –3x2 D y = 1,5x2 E y = 4x2 3 Bestimme a so, dass P auf der Parabel p mit y = ax2 (a X \ {0}) liegt. a) P (1 | –3) b) P ( √ __ 2 | –3) c) P (1,6 I –7,04) d) P (–0,3 I 0,09) e) P ( √ __ 5 | 4) 4 a) Überlege, wie Eva zu dieser Feststellung kommen könnte, ohne dabei eine Zeichnung anzufertigen. b) Entscheide, ob der Punkt oberhalb, unterhalb oder auf dem Graphen liegt. 1 P (4,4 | 7,26) p: y = – 3 __ 8 x 2 2 P (–4,8 | –57,8) p: y = –2,5x2 3 P (–1,5 | 0,45) p: y = 0,2x2 4 P (0,5 | –0,8) p: y = 3,2x2 5 Bestimme die fehlenden Koordinaten so, dass gilt: A, B X p. a) A (–2 | yA ) B (xB | 4) p: y = 3x 2 b) A (xA | –4,9) B (–2 | yB ) p: y = –0,4x 2 Im Folgenden gilt: = Es soll gelten: xA xB . Bremsen Für die Berechnung der Strecke, die ein sich bewegendes Fahrzeug braucht, bis es vollständig zum Stehen gekommen ist, gilt folgende Formel: Anhalteweg = Reaktionsweg + Bremsweg Faustformel für den Reaktionsweg in m: 3 · ( Geschwindigkeit in km ___ h _________________10 ) Faustformel für den Bremsweg in m: 3 __ 4 · ( Geschwindigkeit in km ___ h _________________10 ) 2 • Informiert euch, was genau mit Reaktionsweg und Bremsweg gemeint ist. • Erstellt eine Tabelle für Reaktionsweg, Bremsweg und Anhalteweg für Geschwindigkeiten von 30 km ___ h , 50 km ___ h , 60 km ___ h , 80 km ___ h und 100 km ___ h . • Nehmt Pylonen, Maßbänder (min. 50 m) und stellt für 30 km ___ h und 50 km ___ h alle „drei Wege“ auf dem Pausenhof dar. Der Punkt P (–1,5 | 1,25) liegt oberhalb der Parabel mit der Gleichung y = 1 __ 2 x 2. An ha lt ew eg Reaktionsweg Bremsbeginn Bremsweg Sehen der Gefahr Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs