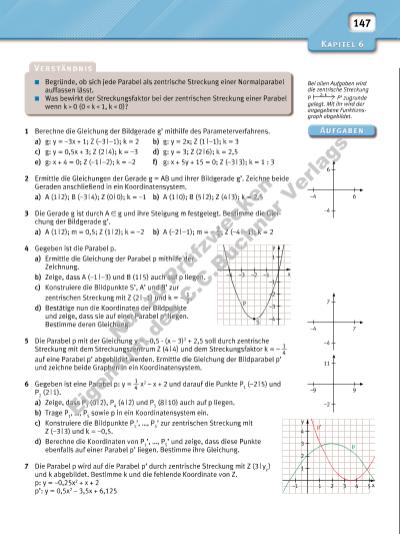
147 1 Berechne die Gleichung der Bildgerade g’ mithilfe des Parameterverfahrens. a) g: y = –3x + 1; Z (–3 | –1); k = 2 b) g: y = 2x; Z (1 | –1); k = 3 c) g: y = 0,5x + 3; Z (2 | 4); k = –3 d) g: y = 3; Z (2 | 6); k = 2,5 e) g: x + 4 = 0; Z (–1 | –2); k = –2 f) g: x + 5y + 15 = 0; Z (–3 | 3); k = 1 : 3 2 Ermittle die Gleichungen der Gerade g = AB und ihrer Bildgerade g’. Zeichne beide Geraden anschließend in ein Koordinatensystem. a) A (1 | 2); B (–3 | 4); Z (0 | 0); k = –1 b) A (1 | 0); B (5 | 2); Z (4 | 3); k = 2,5 3 Die Gerade g ist durch A ∈ g und ihre Steigung m festgelegt. Bestimme die Gleichung der Bildgerade g’. a) A (1 | 2); m = 0,5; Z (1 | 2); k = –2 b) A (–2 | –1); m = – 2 __ 3 ; Z (–4 | –1); k = 2 4 Gegeben ist die Parabel p. a) Ermittle die Gleichung der Parabel p mithilfe der Zeichnung. b) Zeige, dass A (–1 | –3) und B (1 | 5) auch auf p liegen. c) Konstruiere die Bildpunkte S’, A’ und B’ zur zentrischen Streckung mit Z (2 | –1) und k = – 1 __ 2 . d) Bestätige nun die Koordinaten der Bildpunkte und zeige, dass sie auf einer Parabel p’ liegen. Bestimme deren Gleichung. 5 Die Parabel p mit der Gleichung y = –0,5 · (x – 3)2 + 2,5 soll durch zentrische Streckung mit dem Streckungszentrum Z (4 | 4) und dem Streckungsfaktor k = – 1 __ 4 auf eine Parabel p’ abgebildet werden. Ermittle die Gleichung der Bildparabel p’ und zeichne beide Graphen in ein Koordinatensystem. 6 Gegeben ist eine Parabel p: y = 1 __ 4 x 2 – x + 2 und darauf die Punkte P1 (–2 | 5) und P2 (2 | 1). a) Zeige, dass P3 (0 | 2), P4 (4 | 2) und P5 (8 | 10) auch auf p liegen. b) Trage P1, …, P5 sowie p in ein Koordinatensystem ein. c) Konstruiere die Bildpunkte P1’, …, P5’ zur zentrischen Streckung mit Z (–3 | 3) und k = –0,5. d) Berechne die Koordinaten von P1’, …, P5’ und zeige, dass diese Punkte ebenfalls auf einer Parabel p’ liegen. Bestimme ihre Gleichung. 7 Die Parabel p wird auf die Parabel p’ durch zentrische Streckung mit Z (3 | yz ) und k abgebildet. Bestimme k und die fehlende Koordinate von Z. p: y = –0,25x2 + x + 2 p’: y = 0,5x2 – 3,5x + 6,125 Begründe, ob sich jede Parabel als zentrische Streckung einer Normalparabel auffassen lässt. Was bewirkt der Streckungsfaktor bei der zentrischen Streckung einer Parabel wenn k 0 (0 k 1, k 0)? Bei allen Aufgaben wird die zentrische Streckung P Z; k P’ zugrunde gelegt. Mit ihr wird der angegebene Funktionsgraph abgebildet. 6 6–4 –4 7 7–4 –4 11 9–9 –2 –4 –2 –1 S p –4 –3 –3 –2 –1 1 y x 4 –1 1 2 3 4 5 2 3 1 y x p p’ Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C .B uc hn er V er la gs