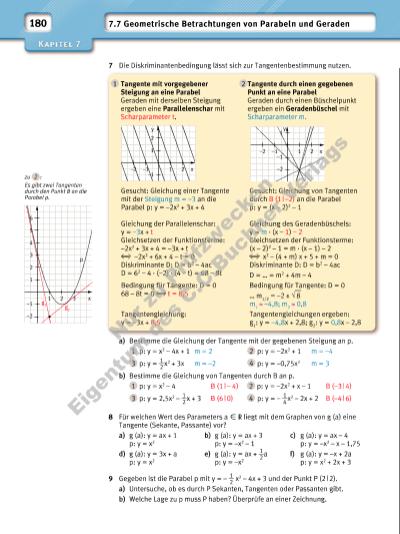
| Volltext anzeigen | |
181 10 Weise nach, dass A (–2 | 1) auf allen Geraden der Schar g (m) liegt, nicht aber auf p. Bestimme die Schnittpunkte Sn von p mit den Geraden der Schar g (m) für m X {–0,5; 0; 0,5; 1; 2; 3}. p: y = (x – 1)2 – 1 g (m): y = m (x + 2) + 1 11 Bei Autorennstrecken gibt es Kurven, deren Verlauf Parabeln gleicht. In der Zeichnung sind eine Parabel p1 und eine Parabelschar p (a) durch eine Strecke [AB] verbunden. p1: y = –0,5x 2 – 2x + 5; p (a): y = a (x – 4)2 – 1; A (2 | 1); B (0 | 5) a) Zeichne p1 sowie A und B in dein Heft. b) Zeige rechnerisch, dass AB Tangente an p1 ist. c) Es sei AB auch Tangente an p (a). Bestimme a. d) Stell dir vor, die Skizze zeige den Verlauf einer Autorennstrecke. 1 Bestimme ___ AB zeichnerisch, wenn gilt: 1 LE 100 m. 2 Berechne die Zeit, die ein Sportwagen für [AB] benötigt, der mit durchschnittlich 180 km ___ h fährt. 12 Die Parabel p: y = – 1 __ 2 x 2 – 2x + 3,5 und die Gerade g: y = –0,5x + 1,5 sind gegeben. a) Zeichne p und g in ein Koordinatensystem. b) Berechne die Nullstellen der beiden Funktionen. c) Berechne die Koordinaten der Schnittpunkte A und B beider Graphen. d) Eine Parallele zu g ist Tangente an die Parabel p. Berechne die Gleichung von t und die Koordinaten des Berührpunktes T. e) Auf dem Parabelbogen liegen zwischen den Punkten A und B die Punkte Cn (x | – 1 __ 2 x 2 – 2x + 3,5). Zeichne das Dreieck ABC1 für x = –1 ein. f) Gib das Intervall für x an, in dem Dreiecke ABCn existieren. g) Berechne den Flächeninhalt der Dreiecke ABCn in Abhängigkeit von x. h) Bestimme den Wert für x so, dass das Dreieck den Flächeninhalt 5 FE hat. i) Das Dreieck ABC0 habe maximalen Flächeninhalt. Bestimme die Koordinaten von C0 und begründe, warum T und C0 identisch sind. 13 Für welchen Wert des Parameters a berührt die Gerade g die zugehörige Scharparabel? Bestimme die Koordinaten des Berührpunktes. Überprüfe zeichnerisch. a) g: y = 2x + 7 b) g: y = –2x + 3 c) g: 2x – y + 2 = 0 p (a): y = (x + 2a)2 p (a): y = x2 + a2 p (a): y = 0,5ax2 d) g: 2x + y + 2 = 0 e) g: y = 4x + 3 f) g: y = –2x + 1 p (a): y = –(x – a)2 p (a): y = –(x – 1)2 + a2 p (a): y = (x – a)2 – 2a 14 Welche nach oben geöffnete Normalparabel, deren Scheitel auf der Gerade g liegt, berührt die Gerade t? a) g: x = 3 b) g: y = –2 c) g: y = x t: y = 2x – 4 t: y = x + 3 t: y = –x Lösung zu 12 g): A (x) = (–1,25x2 – 3,75x + 5) FE Zeichne bei den Parabeln jeweils nur die entsprechenden Abschnitte. 7 6–7 –4 1 1 2 3 4 5 y 2–2 –1 x–3 4 –1 A B 3 6 Nu r z u Pr üf zw ec ke n Ei ge tu m d es C .C .B uc hn er V er la gs | |
 « |  » |
|
» Zur Flash-Version des Livebooks | |