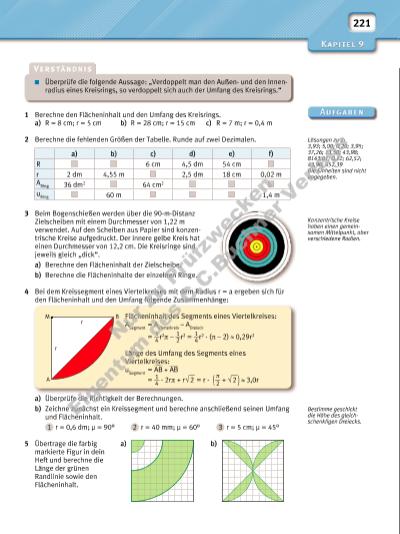
221 1 Berechne den Flächeninhalt und den Umfang des Kreisrings. a) R = 8 cm; r = 5 cm b) R = 28 cm; r = 15 cm c) R = 7 m; r = 0,4 m 2 Berechne die fehlenden Größen der Tabelle. Runde auf zwei Dezimalen. 3 Beim Bogenschießen werden über die 90-m-Distanz Zielscheiben mit einem Durchmesser von 1,22 m verwendet. Auf den Scheiben aus Papier sind konzentrische Kreise aufgedruckt. Der innere gelbe Kreis hat einen Durchmesser von 12,2 cm. Die Kreisringe sind jeweils gleich „dick“. a) Berechne den Flächeninhalt der Zielscheibe. b) Berechne die Flächeninhalte der einzelnen Ringe. 4 Bei dem Kreissegment eines Viertelkreises mit dem Radius r = a ergeben sich für den Flächeninhalt und den Umfang folgende Zusammenhänge: a) Überprüfe die Richtigkeit der Berechnungen. b) Zeichne zunächst ein Kreissegment und berechne anschließend seinen Umfang und Flächeninhalt. 1 r = 0,6 dm; μ = 90° 2 r = 40 mm; μ = 60° 3 r = 5 cm; μ = 45° 5 Übertrage die farbig a) b) markierte Figur in dein Heft und berechne die Länge der grünen Randlinie sowie den Flächeninhalt. Überprüfe die folgende Aussage: „Verdoppelt man den Außenund den Innenradius eines Kreisrings, so verdoppelt sich auch der Umfang des Kreisrings.“ Konzentrische Kreise haben einen gemeinsamen Mittelpunkt, aber verschiedene Radien. a) b) c) d) e) f) R 6 cm 4,5 dm 54 cm r 2 dm 4,55 m 2,5 dm 18 cm 0,02 m ARing 36 dm2 64 cm2 uRing 60 m 1,4 m Flächeninhalt des Segments eines Viertelkreises: ASegment = AViertelkreis – ADreieck = 1 __ 4 r 2π – 1 __ 2 r 2 = 1 __ 4 r 2 · (π – 2) 0,29r2 Länge des Umfang des Segments eines Viertelkreises: uSegment = AB + ___ AB = 1 __ 4 · 2rπ + r √ __ 2 = r · ( π __ 2 + √ __ 2 ) 3,0r M B A r r Lösungen zu 2: 3,93; 5,00; 0,20; 3,95; 37,26; 13,50; 43,98; 8143,01; 0,12; 62,52; 43,98; 452,39 Die Einheiten sind nicht angegeben. Bestimme geschickt die Höhe des gleichschenkligen Dreiecks. Nu r z u Pr üf zw ec ke n Ei ge nt um d C .C .B uc hn er V er la gs