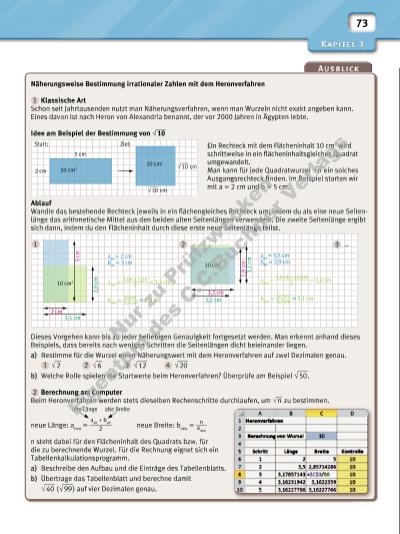
73 10 cm22 cm Start: Ziel: 5 cm 10 cm2 2 cm 3,5 cm 3,5 cm 3,2 cm … 2, 9 cm 5 cm 3, 1 cm 2, 9 cm 10 cm2 10 cm2 1 2 3 aalt = 2 cm balt = 5 cm aalt = 3,5 cm balt = 2,9 cm aneu = 2 cm + 5 cm ________2 = 3,5 cm bneu = 10 cm2 _____3,5 cm 2,9 cm aneu = 3,5 cm + 2,9 cm __________2 = 3,2 cm bneu = 10 cm2 _____3,2 cm 3,1 cm Näherungsweise Bestimmung irrationaler Zahlen mit dem Heronverfahren 1 Klassische Art Schon seit Jahrtausenden nutzt man Näherungsverfahren, wenn man Wurzeln nicht exakt angeben kann. Eines davon ist nach Heron von Alexandria benannt, der vor 2000 Jahren in Ägypten lebte. Idee am Beispiel der Bestimmung von √ ___ 10 Ablauf Wandle das bestehende Rechteck jeweils in ein fl ächengleiches Rechteck um, indem du als eine neue Seitenlänge das arithmetische Mittel aus den beiden alten Seitenlängen verwendest. Die zweite Seiten länge ergibt sich dann, indem du den Flächeninhalt durch diese erste neue Seitenlänge teilst. Dieses Vorgehen kann bis zu jeder beliebigen Genauigkeit fortgesetzt werden. Man erkennt anhand dieses Beispiels, dass bereits nach wenigen Schritten die Seitenlängen dicht beieinander liegen. a) Bestimme für die Wurzel einen Näherungswert mit dem Heronverfahren auf zwei Dezimalen genau. 1 √ __ 2 2 √ __ 6 3 √ ___ 12 4 √ ___ 20 b) Welche Rolle spielen die Startwerte beim Heron verfahren? Überprüfe am Beispiel √ ___ 50 . 2 Berechnung am Computer Beim Heronverfahren werden stets dieselben Rechenschritte durchlaufen, um √ __ n zu bestimmen. neue Länge: aneu = aalt + balt _______2 neue Breite: bneu = n ___ aneu n steht dabei für den Flächeninhalt des Quadrats bzw. für die zu berechnende Wurzel. Für die Rechnung eignet sich ein Tabellenkalkulations programm. a) Beschreibe den Aufbau und die Einträge des Tabellenblatts. b) Übertrage das Tabellenblatt und berechne damit √ ___ 40 ( √ ___ 99 ) auf vier Dezimalen genau. alte Länge alte Breite Ein Rechteck mit dem Flächeninhalt 10 cm2 wird schrittweise in ein fl ächeninhaltsgleiches Quadrat umgewandelt. Man kann für jede Quadratwurzel √ __ n ein solches Ausgangsrechteck fi nden. Im Beispiel starten wir mit a = 2 cm und b = 5 cm. Nu r z u Pr üf zw ck en Ei ge nt um d es C .C .B uc hn er V er la gs