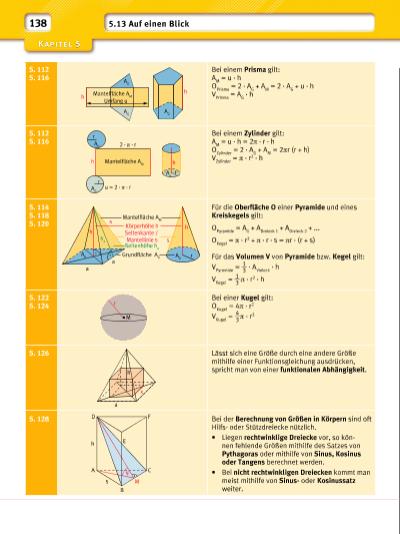
S. 112 S. 116 Bei einem Prisma gilt: A M = u · h O Prisma = 2 · A G + A M = 2 · A G + u · h V Prisma = A G · h S. 112 S. 116 Bei einem Zylinder gilt: A M = u · h = 2π · r · h O Zylinder = 2 · A G + A M = 2πr (r + h) V Zylinder = π · r2 · h S. 114 S. 118 S. 120 Für die Oberfl äche O einer Pyramide und eines Kreiskegels gilt: O Pyramide = A G + A Dreieck 1 + A Dreieck 2 + ... O Kegel = π · r2 + π · r · s = πr · (r + s) Für das Volumen V von Pyramide bzw. Kegel gilt: V Pyramide = 1 __ 3 · AVieleck · h V Kegel = 1 __ 3 π · r2 · h S. 122 S. 124 Bei einer Kugel gilt: O Kugel = 4π · r2 V Kugel = 4 __ 3π · r3 S. 126 Lässt sich eine Größe durch eine andere Größe mithilfe einer Funktionsgleichung ausdrücken, spricht man von einer funktionalen Abhängigkeit. S. 128 Bei der Berechnung von Größen in Körpern sind oft Hilfsoder Stützdreiecke nützlich. • Liegen rechtwinklige Dreiecke vor, so können fehlende Größen mithilfe des Satzes von Pythagoras oder mithilfe von Sinus, Kosinus oder Tangens berechnet werden. • Bei nicht rechtwinkligen Dreiecken kommt man meist mithilfe von Sinusoder Kosinussatz weiter. A G A D h Umfang u Mantelfläche A M A G h rA G A G a a Mantelfläche A M Körperhöhe h h h h a s s Seitenkante / Mantellinie s Grundfläche A G Seitenhöhe h a r r A D Mantelfläche A M h A G 2 · π · r u = 2 · π · r rA G h 138 5.13 Auf einen Blick M r h a x D F C M  A B s h E