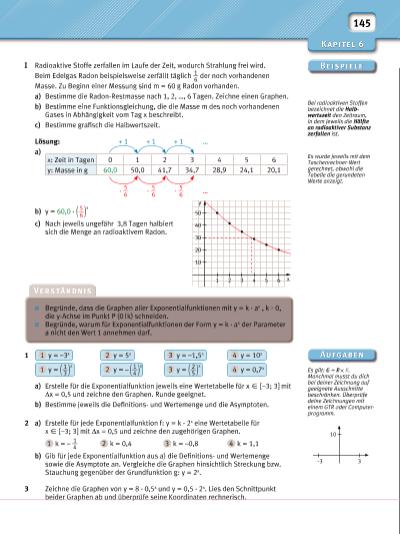
146 6.2 Exponentialfunktionen 4 Gegeben ist die Funktion f: y = 0,5x. a) Bestimme y p so, das der Punkt P (3 | y p ) auf dem Graphen von f liegt. b) Zeichne den Graphen von f und gib seine Eigenschaften an. c) Löse mithilfe des Graphen die Gleichung 0,5x = 7 näherungsweise. 5 a) Zeichne die Graphen der Funktionen f 1 : y = 2x und f 2 : y = 4x mithilfe einer Wertetabelle für x Z [–2; 2] mit Δx = 0,5. b) Auf jeder Parallelen zur x-Achse haben die Punkte P 1 Z f 1 und P 2 Z f 2 die gleichen Entfernungen voneinander wie der Punkt P 2 von der y-Achse. 1 Überprüfe die Aussage an Beispielen. 2 Begründe diesen Sachverhalt. 6 In einem Fernsehquiz, bei dem einem Kandidaten maximal 10 Fragen gestellt werden, kann man zwischen zwei Optionen wählen. Bei einer falschen Antwort geht jeweils der ganze Gewinn verloren. a) Beschreibe die beiden Optionen jeweils durch eine Funktionsgleichung. b) Für welche Option würdest du dich entscheiden? Begründe. 7 Eine Strecke von 1 m Länge wird fortlaufend halbiert. a) Gib eine Gleichung der Form y = ax an, die diesen Vorgang beschreibt. b) Bestimme, nach wie vielen Teilungen man zum ersten Mal eine Strecke von weniger als 1 mm Länge erhält. c) Beschreibe, wie sich die Gleichung aus a) verändert, wenn die Strecke zu Beginn 2 m (4 m, 5 m, 8 m) lang ist. 8 Ein 1000 m2 großer Baggersee wird erweitert. Jede Woche ver größern Bagger die Wasserfl äche um 40 m2. Eine schnell wachsende Algenart wird entdeckt, die zu Beginn eine Fläche von 4 m2 einnimmt. Sie bereitet Sorge, denn sie verdoppelt jede Woche ihre Fläche. a) Stelle das Wachstum der Alge und die Vergrößerung der Wasserfl äche durch den Bagger grafi sch in einem geeigneten Koordinatensystem dar (x-Achse: 1 cm 1 Woche, y-Achse: 1 cm 200 m2). b) Bestimme die Funktionsgleichungen für die beiden Wachstumsvorgänge. c) Bestimme grafi sch, wann die Alge etwa den ganzen See bedeckt. 9 Ein Guthaben von 15 000 f wird jährlich mit 4 % verzinst. a) Wie hoch ist das Guthaben nach 1, 2, …, 10 Jahren? b) Ermittle die Zeit, nach der sich das Guthaben verdoppelt hat. Setze dazu die Reihe aus a) geeignet fort. 1 1–1–2–3–4 2 3 x 2 P 2 P 1 f 1 f 2 3 4 5 6 y Option 1 Der Kandidat hat 100 f Startguthaben. Jede richtige Antwort verdoppelt das Guthaben. Option 2 Jede richtige Antwort bringt 500 f. 8 –3 3 8 –2 2 Die Zinsen werden am Ende jeden Jahres nicht abgehoben, sondern mitverzinst.