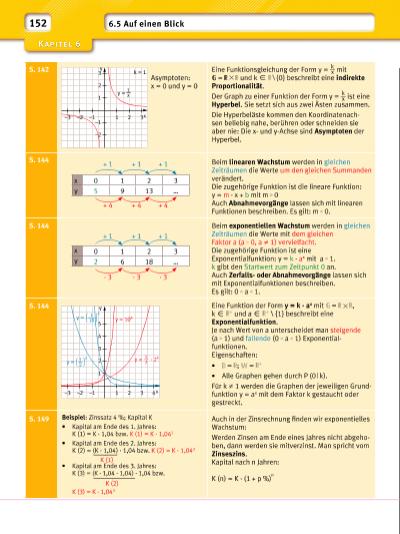
S. 142 Asymptoten: x = 0 und y = 0 Eine Funktionsgleichung der Form y = k __ x mit = und k X \ {0} beschreibt eine indirekte Proportionalität. Der Graph zu einer Funktion der Form y = k __ x ist eine Hyperbel. Sie setzt sich aus zwei Ästen zusammen. Die Hyperbeläste kommen den Koordinatenachsen beliebig nahe, berühren oder schneiden sie aber nie: Die xund y-Achse sind Asymptoten der Hyperbel. S. 144 Beim linearen Wachstum werden in gleichen Zeiträumen die Werte um den gleichen Summanden verändert. Die zugehörige Funktion ist die lineare Funktion: y = m · x + b mit m 0 Auch Abnahmevorgänge lassen sich mit linearen Funktionen beschreiben. Es gilt: m 0. S. 144 Beim exponentiellen Wachstum werden in gleichen Zeiträumen die Werte mit dem gleichen Faktor a (a 0, a ≠ 1) vervielfacht. Die zugehörige Funktion ist eine Exponentialfunktion: y = k · ax mit a 1. k gibt den Startwert zum Zeitpunkt 0 an. Auch Zerfallsoder Abnahmevorgänge lassen sich mit Exponentialfunktionen beschreiben. Es gilt: 0 a 1. S. 144 Eine Funktion der Form y = k · ax mit = , k Z und a Z \ {1} beschreibt eine Exponentialfunktion. Je nach Wert von a unterscheidet man steigende (a 1) und fallende (0 a 1) Exponentialfunktionen. Eigenschaften: • = ; = • Alle Graphen gehen durch P (0 | k). Für k ≠ 1 werden die Graphen der jeweiligen Grundfunktion y = ax mit dem Faktor k gestaucht oder gestreckt. S. 149 Beispiel: Zinssatz 4 %; Kapital K • Kapital am Ende des 1. Jahres: K (1) = K · 1,04 bzw. K (1) = K · 1,041 • Kapital am Ende des 2. Jahres: K (2) = (K · 1,04) · 1,04 bzw. K (2) = K · 1,042 • Kapital am Ende des 3. Jahres: K (3) = (K · 1,04 · 1,04) · 1,04 bzw. K (3) = K · 1,043 Auch in der Zinsrechnung fi nden wir exponentielles Wachstum: Werden Zinsen am Ende eines Jahres nicht abgehoben, dann werden sie mitverzinst. Man spricht vom Zinseszins. Kapital nach n Jahren: K (n) = K · (1 + p %) n y x1–1–2–3 2 3 k = 1 1 –1 2 3 –2 y = 1 x y x1–1–2–3 2 3 4 1 2 3 4 5 y = ( 1 __ 10 ) x y = ( 1 __ 2 ) x y = 1 __ 2 · 2 x y = 10x 152 6.5 Auf einen Blick x 0 1 2 3 y 5 9 13 … + 1 + 4 + 1 + 4 + 1 + 4 x 0 1 2 3 y 2 6 18 … + 1 · 3 + 1 · 3 + 1 · 3 K (1) K (2)