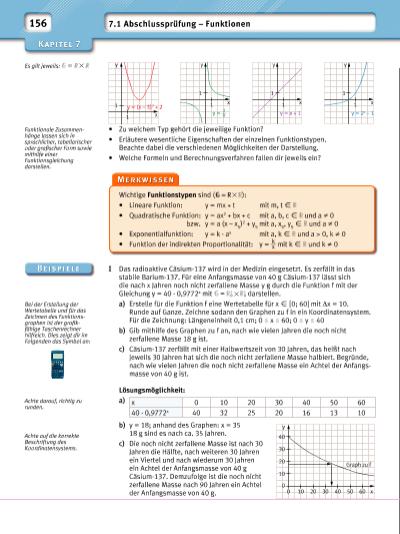
156 7.1 Abschlussprüfung – Funktionen Wichtige Funktionstypen sind ( = ): • Lineare Funktion: y = mx + t mit m, t X • Quadratische Funktion: y = ax2 + bx + c mit a, b, c X und a ≠ 0 bzw. y = a (x – x S )2 + y S mit a, x S , y S X und a ≠ 0 • Exponentialfunktion: y = k · ax mit a, k X und a > 0, k ≠ 0 • Funktion der indirekten Proportionalität: y = k __ x mit k X und k ≠ 0 • Zu welchem Typ gehört die jeweilige Funktion? • Erläutere wesentliche Eigenschaften der einzelnen Funktionstypen. Beachte dabei die verschiedenen Möglichkeiten der Darstellung. • Welche Formeln und Berechnungsverfahren fallen dir jeweils ein? I Das radioaktive Cäsium-137 wird in der Medizin eingesetzt. Es zerfällt in das stabile Barium-137. Für eine Anfangsmasse von 40 g Cäsium-137 lässt sich die nach x Jahren noch nicht zerfallene Masse y g durch die Funktion f mit der Gleichung y = 40 · 0,9772x mit = 0 0 darstellen. a) Erstelle für die Funktion f eine Wertetabelle für x X [0; 60] mit Δx = 10. Runde auf Ganze. Zeichne sodann den Graphen zu f in ein Koordinatensystem. Für die Zeichnung: Längeneinheit 0,1 cm; 0 x 60; 0 y 40 b) Gib mithilfe des Graphen zu f an, nach wie vielen Jahren die noch nicht zerfallene Masse 18 g ist. c) Cäsium-137 zerfällt mit einer Halbwertszeit von 30 Jahren, das heißt nach jeweils 30 Jahren hat sich die noch nicht zerfallene Masse halbiert. Begründe, nach wie vielen Jahren die noch nicht zerfallene Masse ein Achtel der Anfangsmasse von 40 g ist. Lösungsmöglichkeit: a) b) y = 18; anhand des Graphen: x = 35 18 g sind es nach ca. 35 Jahren. c) Die noch nicht zerfallene Masse ist nach 30 Jahren die Hälfte, nach weiteren 30 Jahren ein Viertel und nach wiederum 30 Jahren ein Achtel der Anfangsmasse von 40 g Cäsium-137. Demzufolge ist die noch nicht zerfallene Masse nach 90 Jahren ein Achtel der Anfangsmasse von 40 g. Es gilt jeweils: = Funktionale Zusammenhänge lassen sich in sprachlicher, tabellarischer oder grafi scher Form sowie mithilfe einer Funktionsgleichung darstellen. Bei der Erstellung der Wertetabelle und für das Zeichnen des Funktionsgraphen ist der grafi kfähige Taschenrechner hilfreich. Dies zeigt dir im Folgenden das Symbol an: Achte darauf, richtig zu runden. Achte auf die korrekte Beschriftung des Koordinatensystems. x 0 10 20 30 40 50 60 40 · 0,9772x 40 32 25 20 16 13 10 10 0 100 20 30 40 Graph zu f 50 60 x 20 30 40 y y x y x y x x y 1 1 1 1 1 1 1 1 y = (x – 3)2 + 2 y = 2x – 1y = x + 1y = 2 __ x