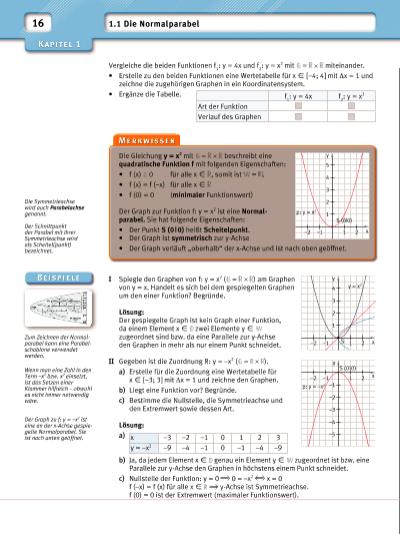
1S–2 –1 1 2 2 3 y = x24 x y –1 –2 –1 1 S (0|0) p: y = –x2 2 –2 –3 –4 –5 x y 1 –2 –1 1 2 2 3 p: y = x2 4 5 x y S (0|0) 16 1.1 Die Normalparabel Vergleiche die beiden Funktionen f 1 : y = 4x und f 2 : y = x2 mit = miteinander. • Erstelle zu den beiden Funktionen eine Wertetabelle für x X [–4; 4] mit Δx = 1 und zeichne die zugehörigen Graphen in ein Koordinatensystem. • Ergänze die Tabelle. I Spiegle den Graphen von f: y = x2 ( = ) am Graphen von y = x. Handelt es sich bei dem gespiegelten Graphen um den einer Funktion? Begründe. Lösung: Der gespiegelte Graph ist kein Graph einer Funktion, da einem Element x X zwei Elemente y X zugeordnet sind bzw. da eine Parallele zur y-Achse den Graphen in mehr als nur einem Punkt schneidet. II Gegeben ist die Zuordnung R: y = –x2 ( = ). a) Erstelle für die Zuordnung eine Wertetabelle für x X [–3; 3] mit Δx = 1 und zeichne den Graphen. b) Liegt eine Funktion vor? Begründe. c) Bestimme die Nullstelle, die Symmetrieachse und den Extremwert sowie dessen Art. Lösung: a) b) Ja, da jedem Element x X genau ein Element y X zugeordnet ist bzw. eine Parallele zur y-Achse den Graphen in höchstens einem Punkt schneidet. c) Nullstelle der Funktion: y = 0 0 = –x2 x = 0 f (–x) = f (x) für alle x X y-Achse ist Symmetrieachse. f (0) = 0 ist der Extremwert (maximaler Funktionswert). Die Gleichung y = x2 mit = beschreibt eine quadratische Funktion f mit folgenden Eigenschaften: • f (x) 0 für alle x X , somit ist = 0 • f (x) = f (–x) für alle x X • f (0) = 0 (minimaler Funktionswert) Der Graph zur Funktion f: y = x2 ist eine Normalparabel. Sie hat folgende Eigenschaften: • Der Punkt S (0 | 0) heißt Scheitelpunkt. • Der Graph ist symmetrisch zur y-Achse • Der Graph verläuft „oberhalb“ der x-Achse und ist nach oben geöffnet. f 1 : y = 4x f 2 : y = x2 Art der Funktion Verlauf des Graphen Die Symmetrieachse wird auch Parabelachse genannt. Der Schnittpunkt der Parabel mit ihrer Symmetrieachse wird als Scheitel(punkt) bezeichnet. Zum Zeichnen der Normalparabel kann eine Parabelschablone verwendet werden. Wenn man eine Zahl in den Term –x2 bzw. x2 einsetzt, ist das Setzen einer Klammer hilfreich – obwohl es nicht immer notwendig wäre. Der Graph zu f: y = –x2 ist eine an der x-Achse gespiegelte Normalparabel. Sie ist nach unten geöffnet. x –3 –2 –1 0 1 2 3 y = –x2 –9 –4 –1 0 –1 –4 –9