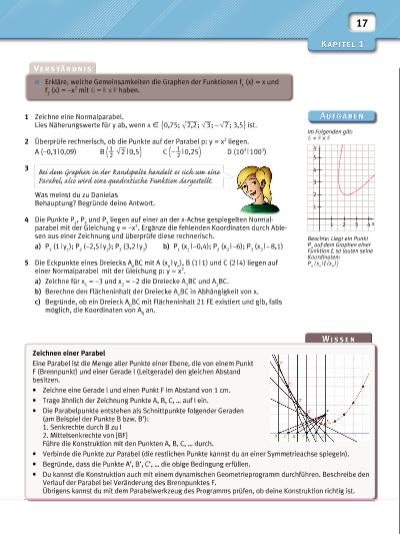
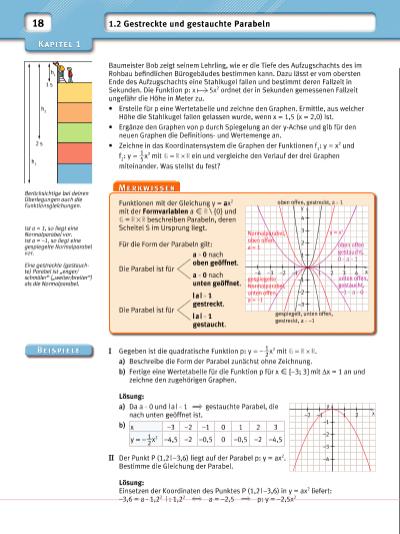
–1 –2 –1 1 2 –2 –3 –4 x y 1 s 2 s h 1 h 2 h 3 1 y = x2 –1 –3–4 –2 –1 1 2 3 4 –2 –3 2 3 4 oben offen gestaucht, 0 a 1 unten offen, gestaucht, –1 a 0 gespiegelt, unten offen, gestreckt, a –1 gespiegelte Normalparabel, unten offen, a = –1 Normalparabel, oben offen a = 1 oben offen, gestreckt, a 1 x y 18 1.2 Gestreckte und gestauchte Parabeln Baumeister Bob zeigt seinem Lehrling, wie er die Tiefe des Aufzugschachts des im Rohbau befi ndlichen Bürogebäudes bestimmen kann. Dazu lässt er vom obersten Ende des Aufzugschachts eine Stahlkugel fallen und bestimmt deren Fallzeit in Sekunden. Die Funktion p: x 5x2 ordnet der in Sekunden gemessenen Fallzeit ungefähr die Höhe in Meter zu. • Erstelle für p eine Wertetabelle und zeichne den Graphen . Ermittle, aus welcher Höhe die Stahlkugel fallen gelassen wurde, wenn x = 1,5 (x = 2,0) ist. • Ergänze den Graphen von p durch Spiegelung an der y-Achse und gib für den neuen Graphen die Defi nitionsund Wertemenge an. • Zeichne in das Koordinatensystem die Graphen der Funktionen f 1 : y = x2 und f 2 : y = 1 __ 5 x 2 mit = ein und vergleiche den Verlauf der drei Graphen miteinander. Was stellst du fest? Berücksichtige bei deinen Überlegungen auch die Funktionsgleichungen. Ist a = 1, so liegt eine Normalparabel vor. Ist a = –1, so liegt eine gespiegelte Normalparabel vor. Eine gestreckte (gestauchte) Parabel ist „enger/ schmäler“ („weiter/breiter“) als die Normalparabel. Funktionen mit der Gleichung y = ax2 mit der Formvariablen a X \ {0} und = beschreiben Parabeln, deren Scheitel S im Ursprung liegt. Für die Form der Parabeln gilt: Die Parabel ist für Die Parabel ist für a 0 nach oben geöffnet. a 0 nach unten geöffnet. | a | 1 gestreckt. | a | 1 gestaucht. I Gegeben ist die quadratische Funktion p: y = – 1 __ 2 x 2 mit = . a) Beschreibe die Form der Parabel zunächst ohne Zeichnung. b) Fertige eine Wertetabelle für die Funktion p für x X [–3; 3] mit Δx = 1 an und zeichne den zugehörigen Graphen. Lösung: a) Da a 0 und | a | 1 gestauchte Parabel, die nach unten geöffnet ist. b) II Der Punkt P (1,2 | –3,6) liegt auf der Parabel p: y = ax2. Bestimme die Gleichung der Parabel. Lösung: Einsetzen der Koordinaten des Punktes P (1,2 | –3,6) in y = ax2 liefert: –3,6 = a · 1,22 | : 1,22 a = –2,5 p: y = –2,5x2 x –3 –2 –1 0 1 2 3 y = – 1 __ 2 x 2 –4,5 –2 –0,5 0 –0,5 –2 –4,5