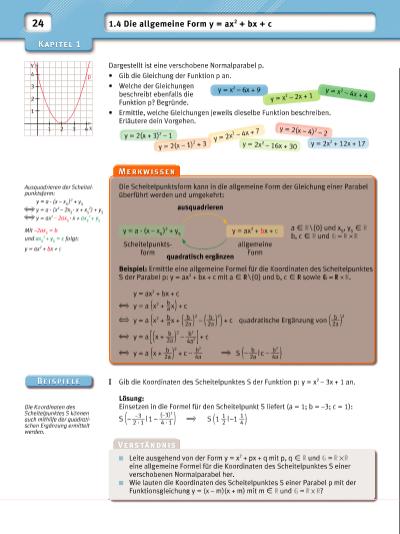
y = x2 – 6x + 9 y = x 2 – 2x + 1 y = x2 – 4x + 4 1 1 2 3 4 2 3 4 x p y 24 1.4 Die allgemeine Form y = ax2 + bx + c Dargestellt ist eine verschobene Normalparabel p. • Gib die Gleichung der Funktion p an. • Welche der Gleichungen beschreibt ebenfalls die Funktion p? Begründe. • Ermittle, welche Gleichungen jeweils dieselbe Funktion beschreiben. Erläutere dein Vorgehen. Ausquadrieren der Scheitelpunktsform: y = a · (x – x S )2 + y S y = a · (x2 – 2x S · x + x S 2) + y S y = ax2 – 2ax S · x + ax S 2 + y S Mit –2ax S = b und ax S 2 + y S = c folgt: y = ax2 + bx + c Die Koordinaten des Scheitelpunktes S können auch mithilfe der quadratischen Ergänzung ermittelt werden. Die Scheitelpunktsform kann in die allgemeine Form der Gleichung einer Parabel überführt werden und umgekehrt: Beispiel: Ermittle eine allgemeine Formel für die Koordinaten des Scheitelpunktes S der Parabel p: y = ax2 + bx + c mit a X \ {0} und b, c X sowie = . y = ax2 + bx + c y = a ( x2 + b __ a x ) + c y = a ( x2 + b __ a x + ( b ___ 2a ) 2 – ( b ___ 2a ) 2 ) + c quadratische Ergänzung von ( b ___ 2a ) 2 y = a [ ( x + b ___ 2a ) 2 – b 2 ___ 4a2 ] + c y = a ( x + b ___ 2a ) 2 + c – b 2 ___ 4a S ( – b ___ 2a | c – b 2 ___ 4a ) y = a · (x – x S )2 + y S y = ax2 + bx + c allgemeine Form Scheitelpunktsform a X \ {0} und x S , y S X b, c X und = quadratisch ergänzen ausquadrieren I Gib die Koordinaten des Scheitelpunktes S der Funktion p: y = x2 – 3x + 1 an. Lösung: Einsetzen in die Formel für den Scheitelpunkt S liefert (a = 1; b = –3; c = 1): S ( – –3 ____ 2 · 1 | 1 – (–3)2 ____4 · 1 ) S ( 1 1 __ 2 | –1 1 __ 4 ) Leite ausgehend von der Form y = x2 + px + q mit p, q X und = eine allgemeine Formel für die Koordinaten des Scheitelpunktes S einer verschobenen Normalparabel her. Wie lauten die Koordinaten des Scheitelpunktes S einer Parabel p mit der Funktionsgleichung y = (x – m)(x + m) mit m X und = ? y = 2(x + 3)2 – 1 y = 2x2 – 16x + 30 y = 2x 2 – 4x + 7 y = 2x2 + 12x + 17y = 2(x – 1) 2 + 3 y = 2(x – 4)2 – 2