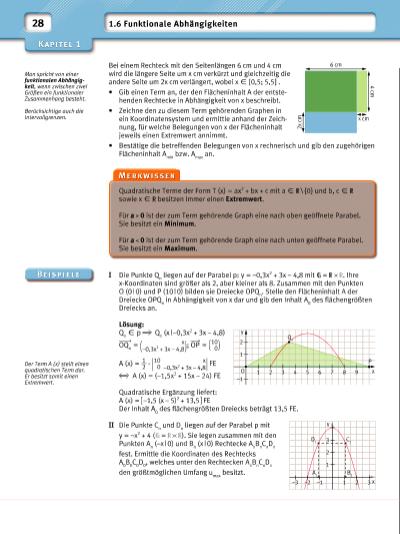
6 cm 4 cm 2 x cm x cm 1 O Q 1 P –1 1 2 3 4 5 6 7 8 9 2 x y 1 A 1 B 1 D 1 C 1 –3 –2 –1 1 2 3 2 3 x y 28 1.6 Funktionale Abhängigkeiten Bei einem Rechteck mit den Seitenlängen 6 cm und 4 cm wird die längere Seite um x cm verkürzt und gleichzeitig die andere Seite um 2x cm verlängert, wobei x X [0,5; 5,5] 0 . • Gib einen Term an, der den Flächeninhalt A der entstehenden Rechtecke in Abhängigkeit von x beschreibt. • Zeichne den zu diesem Term gehörenden Graphen in ein Koordinatensystem und ermittle anhand der Zeichnung, für welche Belegungen von x der Flächeninhalt jeweils einen Extremwert annimmt. • Bestätige die betreffenden Belegungen von x rechnerisch und gib den zugehörigen Flächeninhalt A min bzw. A max an. Man spricht von einer funktionalen Abhängigkeit, wenn zwischen zwei Größen ein funktionaler Zusammenhang besteht. Berücksichtige auch die Intervallgrenzen. Quadratische Terme der Form T (x) = ax2 + bx + c mit a X \ {0} und b, c X sowie x X besitzen immer einen Extremwert. Für a 0 ist der zum Term gehörende Graph eine nach oben geöffnete Parabel. Sie besitzt ein Minimum. Für a 0 ist der zum Term gehörende Graph eine nach unten geöffnete Parabel. Sie besitzt ein Maximum. I Die Punkte Q n liegen auf der Parabel p: y = –0,3x2 + 3x – 4,8 mit = . Ihre x-Koordinaten sind größer als 2, aber kleiner als 8. Zusammen mit den Punkten O (0 | 0) und P (10 | 0) bilden sie Dreiecke OPQ n . Stelle den Flächeninhalt A der Dreiecke OPQ n in Abhängigkeit von x dar und gib den Inhalt A 0 des fl ächengrößten Dreiecks an. Lösung: Q n X p Q n (x | –0,3x2 + 3x – 4,8) _______ › OQ n = ( x –0,3x2 + 3x – 4,8 ) ; _____ › OP = ( 10 0 ) A (x) = 1 __ 2 · | 10 0 x –0,3x2 + 3x – 4,8 | FE A (x) = (–1,5x2 + 15x – 24) FE Quadratische Ergänzung liefert: A (x) = [ –1,5 (x – 5)2 + 13,5 ] FE Der Inhalt A 0 des fl ächengrößten Dreiecks beträgt 13,5 FE. II Die Punkte C n und D n liegen auf der Parabel p mit y = –x2 + 4 ( = ). Sie legen zusammen mit den Punkten A n (–x | 0) und B n (x | 0) Rechtecke A n B n C n D n fest. Ermittle die Koordinaten des Rechtecks A 0 B 0 C 0 D 0 , welches unter den Rechtecken A n B n C n D n den größtmöglichen Umfang u max besitzt. Der Term A (x) stellt einen quadratischen Term dar. Er besitzt somit einen Extremwert.