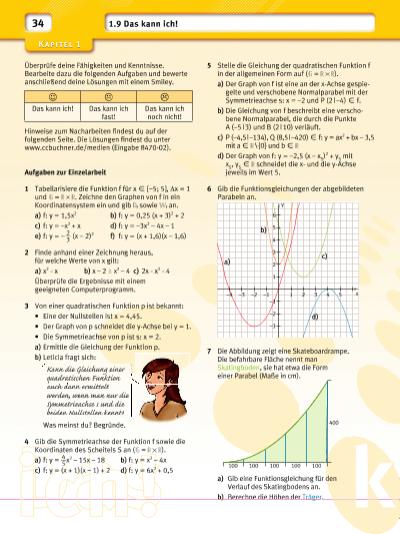
Das kich! 1 –1 –3–4 –2 –1 1 2 3 4 5 –2 –3 2 3 4 5 6 x y a) b) c) d) Kann die Gleichung einer quadratischen Funktion auch dann ermittelt werden, wenn man nur die Symmetrieachse s und die beiden Nullstellen kennt? 34 5 Stelle die Gleichung der quadratischen Funktion f in der allgemeinen Form auf ( = ). a) Der Graph von f ist eine an der x-Achse gespiegelte und verschobene Normalparabel mit der Symmetrieachse s: x = –2 und P (2 | –4) X f. b) Die Gleichung von f beschreibt eine verschobene Normalparabel, die durch die Punkte A (–5 | 3) und B (2 | 10) verläuft. c) P (–4,5 | –134), Q (8,5 | –420) X f: y = ax2 + bx – 3,5 mit a X \ {0} und b X d) Der Graph von f: y = –2,5 (x – x S )2 + y S mit x S , y S X schneidet die xund die y-Achse jeweils im Wert 5. 6 Gib die Funktions gleichungen der abgebildeten Parabeln an. 7 Die Abbildung zeigt eine Skateboardrampe. Die befahrbare Fläche nennt man Skatingboden, sie hat etwa die Form einer Parabel (Maße in cm). a) Gib eine Funktionsgleichung für den Verlauf des Skatingbodens an. b) Berechne die Höhen der Träger. Überprüfe deine Fähigkeiten und Kenntnisse. Bearbeite dazu die folgenden Aufgaben und bewerte anschließend deine Lösungen mit einem Smiley. Hinweise zum Nacharbeiten fi ndest du auf der folgenden Seite. Die Lösungen fi ndest du unter www.ccbuchner.de/medien (Eingabe 8470-02). Aufgaben zur Einzelarbeit 1 Tabellarisiere die Funktion f für x X [–5; 5], Δx = 1 und = . Zeichne den Graphen von f in ein Koordinatensystem ein und gib f sowie f an. a) f: y = 1,5x2 b) f: y = 0,25 (x + 3)2 + 2 c) f: y = –x2 + x d) f: y = –3x2 – 4x – 1 e) f: y = – 2 __ 3 (x – 2) 2 f) f: y = (x + 1,6)(x – 1,6) 2 Finde anhand einer Zeichnung heraus, für welche Werte von x gilt: a) x2 x b) x – 2 x2 – 4 c) 2x x2 4 Überprüfe die Ergebnisse mit einem geeigneten Computerprogramm. 3 Von einer quadratischen Funktion p ist bekannt: • Eine der Nullstellen ist x = 4,45. • Der Graph von p schneidet die y-Achse bei y = 1. • Die Symmetrieachse von p ist s: x = 2. a) Ermittle die Gleichung der Funktion p. b) Leticia fragt sich: Was meinst du? Begründe. 4 Gib die Symmetrieachse der Funktion f sowie die Koordinaten des Scheitels S an ( = ). a) f: y = 4 __ 5 x 2 – 15x – 18 b) f: y = x2 – 4x c) f: y = (x + 1)(x – 1) + 2 d) f: y = 6x2 + 0,5 J K L Das kann ich! Das kann ich fast! Das kann ich noch nicht! 1.9 Das kann ich! 100 100 100 100 100 400