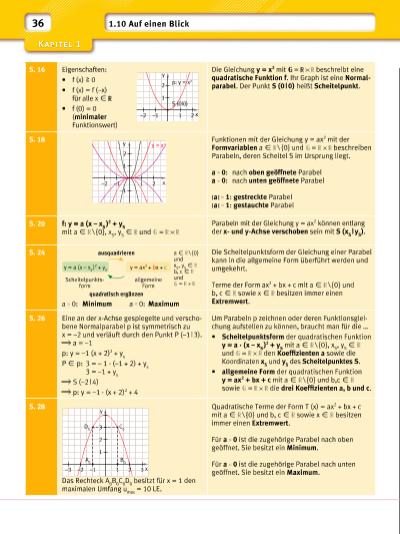
S. 16 Eigenschaften: • f (x) 0 • f (x) = f (–x) für alle x X • f (0) = 0 (minimaler Funktionswert) Die Gleichung y = x2 mit = beschreibt eine quadratische Funktion f. Ihr Graph ist eine Normalparabel. Der Punkt S (0 | 0) heißt Scheitelpunkt. S. 18 Funktionen mit der Gleichung y = ax2 mit der Formvariablen a X \ {0} und = beschreiben Parabeln, deren Scheitel S im Ursprung liegt. a 0: nach oben geöffnete Parabel a 0: nach unten geöffnete Parabel | a | 1: gestreckte Parabel | a | 1: gestauchte Parabel S. 20 f: y = a (x – x S )2 + y S mit a X \ {0}, x S , y S X und = Parabeln mit der Gleichung y = ax2 können entlang der xund y-Achse verschoben sein mit S (x S | y S ). S. 24 a 0: Minimum a 0: Maximum Die Scheitelpunktsform der Gleichung einer Parabel kann in die allgemeine Form überführt werden und umgekehrt. Terme der Form ax2 + bx + c mit a X \ {0} und b, c X sowie x X besitzen immer einen Extremwert. S. 26 Eine an der x-Achse gespiegelte und verschobene Normalparabel p ist symmetrisch zu x = –2 und verläuft durch den Punkt P (–1 | 3). a = –1 p: y = –1 (x + 2)2 + y s P X p: 3 = – 1 · (–1 + 2) + y s 3 = –1 + y s S (–2 | 4) p: y = –1 · (x + 2)2 + 4 Um Parabeln p zeichnen oder deren Funktionsgleichung aufstellen zu können, braucht man für die … • Scheitelpunktsform der quadratischen Funktion y = a · (x – x S )2 + y S mit a X \ {0}, x S , y S X und = den Koeffi zienten a sowie die Ko ordinaten x S und y S des Scheitelpunktes S. • allgemeine Form der quadratischen Funktion y = ax2 + bx + c mit a X \ {0} und b,c X sowie = die drei Koeffi zienten a, b und c. S. 28 Das Rechteck A 0 B 0 C 0 D 0 besitzt für x = 1 den maximalen Umfang u max = 10 LE. Quadratische Terme der Form T (x) = ax2 + bx + c mit a X \ {0} und b, c X sowie x X besitzen immer einen Extremwert. Für a 0 ist die zugehörige Parabel nach oben geöffnet. Sie besitzt ein Minimum. Für a 0 ist die zugehörige Parabel nach unten geöffnet. Sie besitzt ein Maximum. 1 –2 –1 1 2 2 y p: y = x2 x S (0|0) 1 y = x2 –1 –2 –1 1 2 2 x y 1 A 0 B 0 D 0 C 0 –3 –2 –1 1 2 3 2 3 x y 36 1.10 Auf einen Blick y = a (x – x S )2 + y S y = ax2 + bx + c allgemeine Form Scheitelpunktsform a X \ {0} und x S , y S X b, c X und = quadratisch ergänzen ausquadrieren